Junhee Kim

I’m studying Bayesian ML, DL in Bayes Inference LAB, INHA University

8 분 소요

이 포스팅은 “Bayesian Graph Convolutional Neural Networks for Semi-supervised Classification” 논문을 읽고 BGCNN에 대해 정리한 글입니다.

Introduction

그래프는 소셜 네트워크, 분자 구조, 교통망 등 세상의 복잡한 관계를 표현하는 강력한 도구입니다. 주변 노드들의 정보를 모아 자신의 정보를 업데이트하는 방식의 그래프 컨볼루션 신경망(GCNs)은 이러한 그래프 데이터를 처리하는 데 엄청난 성공을 거두며, 노드 분류나 관계 예측 같은 분야에서 뛰어난 성능을 보여주고 있습니다.

GCNs에 대한 설명은 이 글을 참고해주세요.

하지만 GCNN 에서는 주어진 그래프 구조는 Ground Truth 이라는 가정이 존재합니다. 즉, 모델은 노드 간의 연결이 절대적으로 옳다고 가정하고 학습을 진행합니다.

하지만 현실 세계의 데이터는 그렇지 않을 수 있습니다. 친구 추천이 누락되거나(Missing edges), 사실은 아무 관계가 없는데 연결된(Spurious edges) 경우가 존재합니다. 이렇게 노이즈가 낀 불완전한 그래프를 GCNN에 그대로 넣는 것은 예측 성능을 떨어뜨리는 주된 원인이 됩니다.

이러한 한계를 극복하고자 본 논문에서는 그래프 구조 자체의 불확실성을 모델링하는 방법론을 제안합니다.

What is BGCNN?

BGCNN의 핵심 아이디어는 간단합니다. “주어진 그래프를 맹신하지 말고, 가능한 모든 그래프를 고려하자.”

기존 GCN이 관찰된 그래프($G_{obs}$)를 유일한 ‘정답’으로 간주했다면, BGCNN은 이를 숨겨진 ‘진짜 정답’(G)에 대한 하나의 단서일 뿐이라고 봅니다. 즉, 우리가 관찰한 노이즈 낀 그래프는 수많은 가능성 중 하나가 발현된 결과라는 것입니다.

따라서 BGCNN은 관찰된 그래프를 바탕으로, 이 단서를 만들어냈을 법한 수많은 가능한 그래프들의 분포(distribution over graphs) 를 통계적으로 추론합니다.

그리고 이 가상의 그래프들 위에서 GCN 예측을 종합함으로써, 그래프 구조의 불확실성과 모델 파라미터의 불확실성을 모두 끌어안는 훨씬 더 강건한 예측을 만들어냅니다. 결국, 단 하나의 불완전한 지도에 의존하는 대신, 통계적으로 그럴듯한 여러 그래프를 종합하여 최종 결론을 내리는 방식입니다.

한마디로 요약해보자면, 그래프 단위의 Monte Carlo라고 할 수 있겠습니다.

How BGCNN Works (Simple)

BGCNN은 이 복잡한 추론 과정을 몬테카를로 근사라는 강력한 통계적 샘플링 기법을 통해 수행합니다. 전체 과정은 다음과 같이 요약할 수 있습니다.

Step 1: Learn Graph Distribution

먼저, 관찰된 그래프($G_{obs}$)를 가장 잘 설명할 수 있는 확률적 그래프 모델의 파라미터($λ$)를 추론합니다. 논문에서는 a-MMSBM이라는 모델을 사용하는데, 이는 각 노드가 여러 커뮤니티에 속할 수 있고, 같은 커뮤니티끼리 더 잘 연결된다는 보편적인 상식을 모델링합니다. 이 과정을 통해 ‘어떤 노드들이 어떤 커뮤니티에 속하며, 커뮤니티 내/간 연결 확률은 이 정도 될 것이다’라는 그래프 생성 규칙을 학습합니다.

Step 2: Sample Graphs

앞서 학습한 생성 규칙($p(G∣λ)$)에 따라, 진짜 그래프일 가능성이 있는 여러 개의 가상 그래프($G_1, \dots, G_{N_{G}}$)를 샘플링합니다. 이 그래프들은 관찰된 그래프와 비슷하지만, 노이즈가 제거되거나 누락된 엣지가 복원된 다양한 버전이라고 간주할 수 있습니다.

Step 3: Sample Weights & Predic

샘플링된 각각의 그래프($G_i$)위애서 베이지안 GCN을 학습시킵니다. 여기서 모델 가중치($W$)의 불확실성은 MC Dropout을 통해 모델링합니다. 즉, 하나의 그래프($G_i$)에 대해서도 드롭아웃을 통해서 여러 버전의 가중치($W_{s,i}$)를 샘플링하고 각각의 예측 결과를 얻습니다.

Step 4: Aggregate Prediction

마지막으로, 수많은 가상 그래프들($G_i$) 과 각 그래프에 대한 여러 가중치들($W_{s,i}$) 로부터 얻은 모든 예측 결과를 전부 평균냅니다. 이 과정을 수식으로 표현하면 다음과 같습니다. 그래프 구조($G$)와 가중치($W$)의 불확실성을 모두 적분하여 최종 예측 확률을 구하는 것입니다.

\[p(Z|Y_L, X, G_{obs}) \approx \dfrac{1}{N_GS}\sum_{i=1}^{N_G}\sum_{s=1}^S p(Z|W_{s,i}, G_i, X)\]

이러한 과정을 통해 BGCNN은 단 하나의 불완전한 그래프에 의존하는 대신, 통계적으로 그럴듯한 수많은 시나리오를 종합하여 최종 결론을 내리게 됩니다.

How Uncertainty is Generated

BGCNN이 측정하는 불확실성은 기존 베이지안 신경망(BNN)과는 차별화된, 두 가지의 깊이를 가집니다.

1. Structural Uncertainty

이는 그래프 구조 자체의 불확실성에서 비롯됩니다. 만약 샘플링된 여러 가상 그래프($G_i$)에 따라 모델의 예측 결과가 크게 달라진다면, 이는 모델이 현재의 그래프 구조를 별로 신뢰하지 못하며, 특정 엣지(연결)의 존재 여부가 예측에 큰 영향을 미치고 있다는 뜻입니다.

예를 들어, 어떤 노드의 예측 결과가 ‘A’라는 엣지가 있을 땐 90% 확률로 ‘긍정’이었다가, ‘A’ 엣지가 없는 다른 샘플 그래프에선 30%로 뚝 떨어진다면, 바로 이 ‘A’ 엣지 자체가 불확실성의 핵심 원인인 것입니다.

2. Weight Uncertainty

이는 모델 파라미터의 불확실성으로, 전통적인 BNN이 다루는 불확실성입니다. 하나의 고정된 그래프 위에서도, MC Dropout을 통해 얻은 여러 가중치($W_{s,i}$)에 따라 예측 결과들이 흔들릴 수 있습니다. 이는 주로 학습 데이터가 부족하여 모델이 특정 패턴을 확신하지 못할 때 발생합니다.

BGCNN은 이 두 가지 불확실성을 자연스럽게 통합합니다. 따라서 “이 노드의 연결 관계가 애매해서 예측이 흔들리는 건지”, 아니면 “연결 관계는 확실한데 데이터가 부족해서 예측이 흔들리는 건지”를 종합적으로 고려한, 훨씬 더 풍부하고 신뢰도 높은 불확실성을 제공할 수 있습니다.

A Deeper Dive: Methodology

BGCNN의 핵심 아이디어를 조금 더 깊은 수식의 관점에서 살펴보겠습니다.

1.The Goal: Posterior Calculation

BGCNN의 최종 목표는 주어진 정보($Y_L, X, G_{obs}$)를 바탕으로 레이블되지 않은 노드($Z$)의 확률 분포, 즉 사후 확률(Posterior) $p(Z|Y_L, X, G_{obs})$를 계산하는 것입니다. 이 과정을 통해 불확실성을 모두 고려한 최종 예측을 얻을 수 있습니다. 전체 과정이 아래의 적분식 하나에 포함되어있습니다.

\[p(Z|Y_L, X, G_{obs}) = \int p(Z|W, G, X)p(W|Y_L, X, G)p(G|\lambda)p(\lambda|G_{obs}) dW dG d\lambda\]
  1. \(p(\lambda|G_{obs})\): 관찰된 그래프(\(G_{obs}\))로부터 그래프 생성 규칙(\(\lambda\))을 추론하고
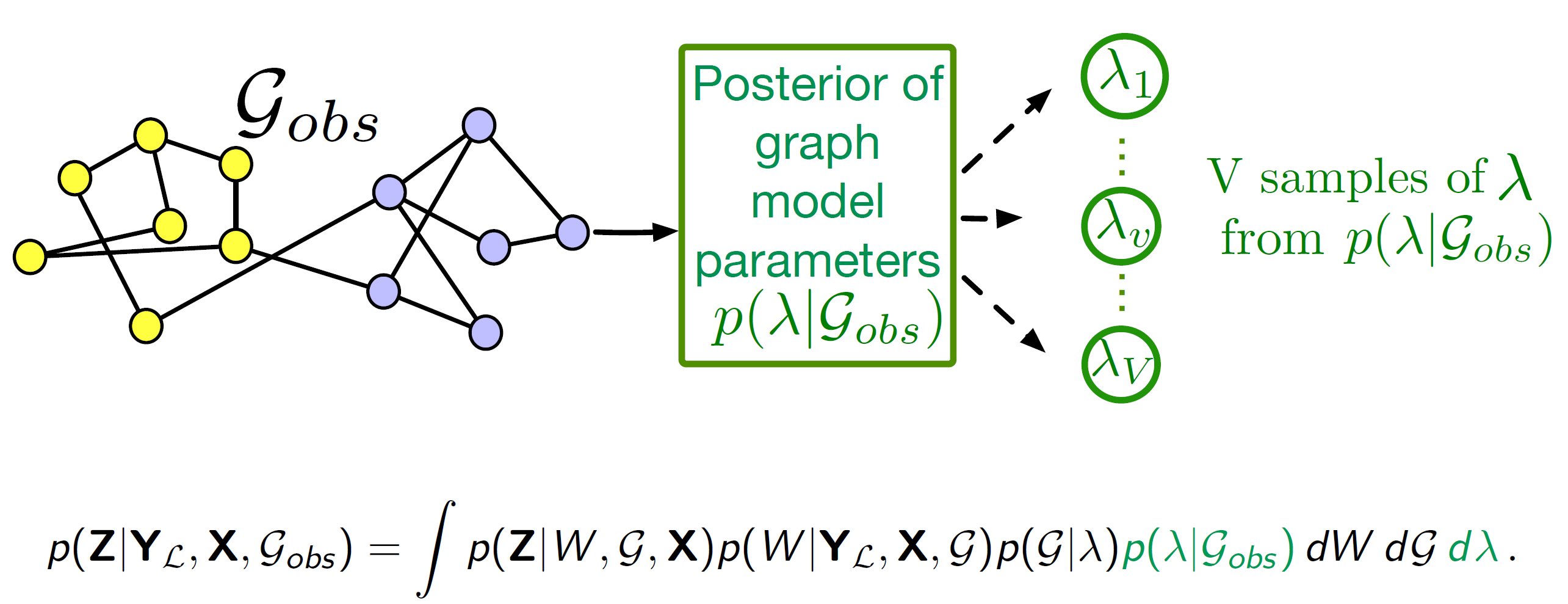
    Step 1: Inferring graph model parameters from the observed graph
  2. \(p(G|\lambda)\): 그 규칙으로 가능한 진짜 그래프(\(G\))들을 만들고
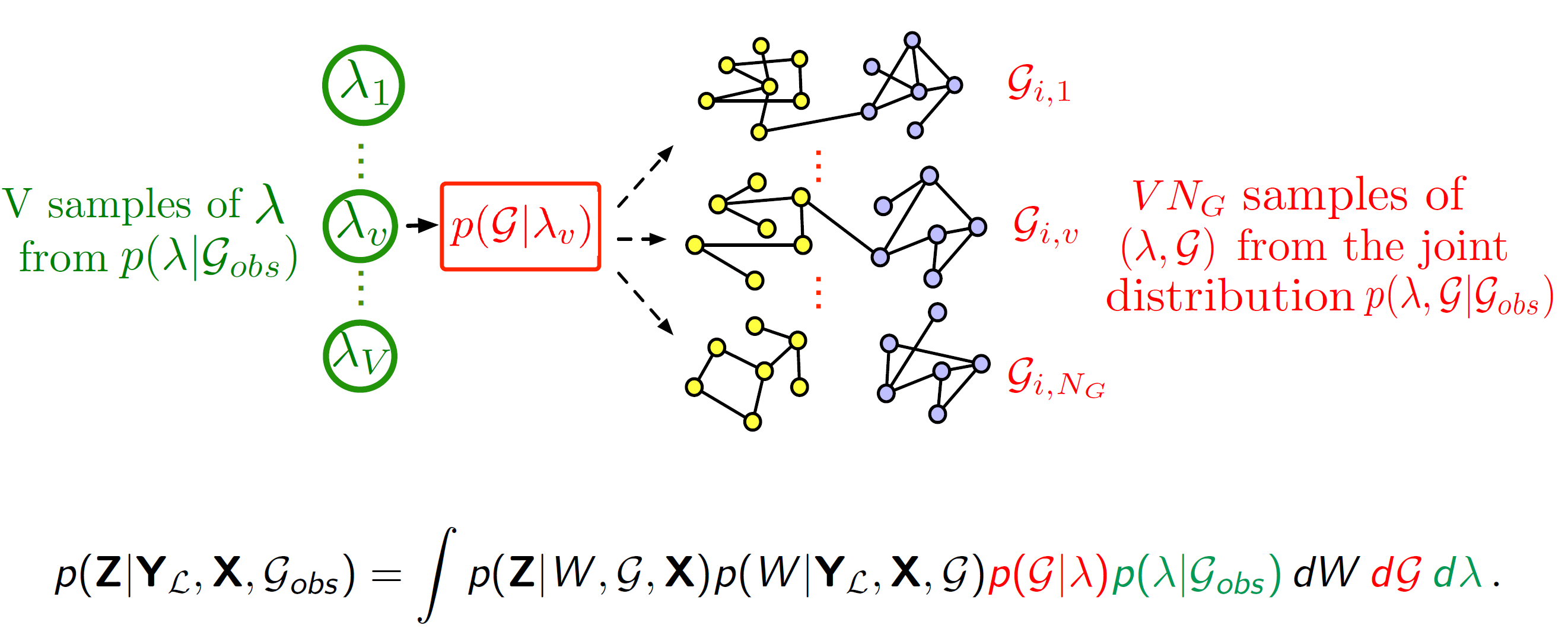
    Step 2: Sampling multiple graph candidates from the parameters
  3. \(p(W|Y_L, X, G)\): 각각의 진짜 그래프 위에서 학습된 GCN 가중치(\(W\))를 추론하고
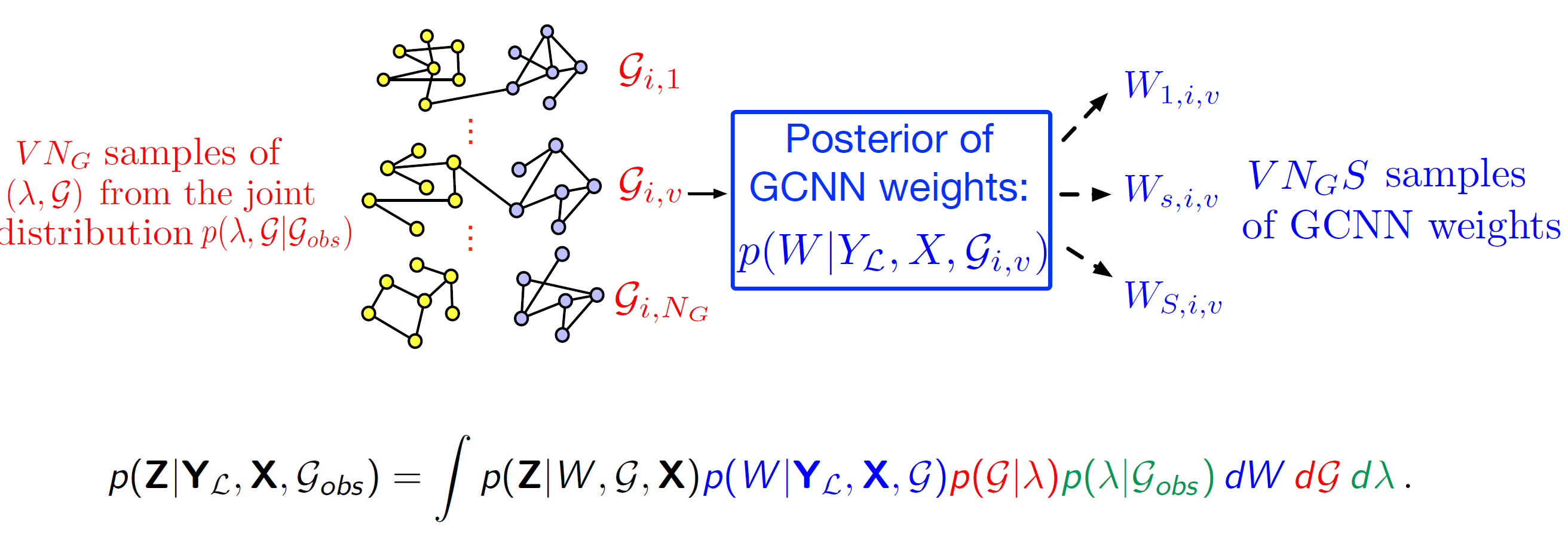
    Step 3: Sampling GCNN weights for each sampled graph
  4. \(p(Z|W, G, X)\): 최종적으로 모든 불확실성을 고려하여 예측(\(Z\))을 수행합니다.

이 모든 단계의 불확실성(\(dW, dG, d\lambda\))을 적분해야만 우리가 원하는 최종 예측 분포를 얻을 수 있습니다.

2. A Practical Solution: Monte Carlo Approximation

위의 적분은 수학적으로 완벽하지만, 모든 경우의 수를 고려해야 하므로 현실적으로 계산이 불가능(intractable)합니다. 그래서 우리는 샘플링을 통해 근사치를 계산하는 몬테카를로(Monte Carlo) 기법을 사용합니다. 이는 앞서 How BGCNN Works 섹션에서 설명한 4단계 과정의 수학적 표현입니다.

\[p(Z|Y_L,X, G_{obs}) \approx \dfrac{1}{N_G S}\sum_{i=1}^{N_G}\sum_{s=1}^S p(Z|W_{s,i}, G_i, X)\]

복잡한 적분 대신, $\lambda$로부터 그래프 $G_i$를 샘플링하고, 각 $G_i$에 대해 가중치 $W_{s,i}$를 샘플링하여 얻은 예측값들을 모두 평균내어 근사하는 것입니다.

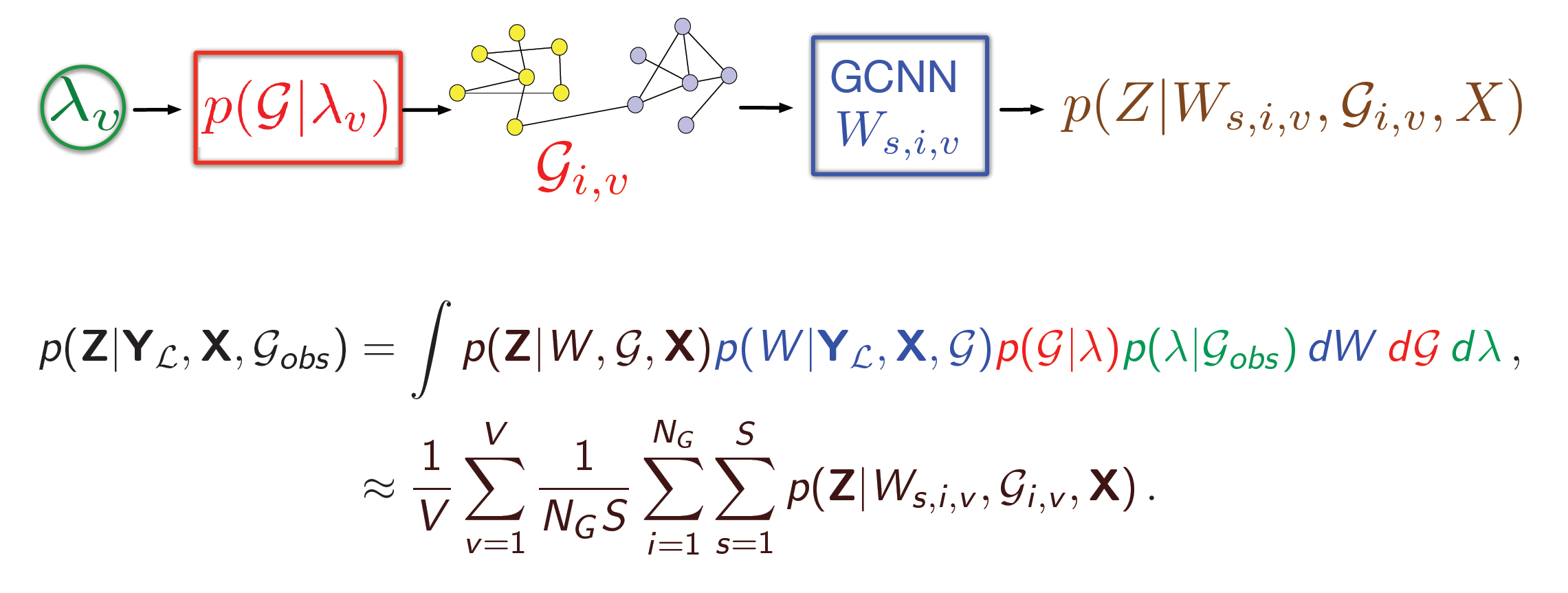
Step 4: The full Monte Carlo approximation process and final formula

3. Graph Modeling: a-MMSBM

BGCNN은 a-MMSBM (assortative Mixed-Membership Stochastic Block Model)이라는 확률적 그래프 생성 모델을 사용하여 그래프의 불확실성을 모델링합니다. 이 모델은 현실 세계의 네트워크가 종종 커뮤니티 구조를 가진다는 점에서 착안합니다.

Assumption

  • Mixed-Membership: 각 노드는 하나의 커뮤니티가 아닌, 여러 커뮤니티에 걸쳐 소속될 수 있습니다. (예: 한 사람은 ‘회사 동료’이면서 ‘대학 동문’ 커뮤니티에 속할 수 있습니다.)
  • Assortative: “끼리끼리 뭉친다”는 아이디어입니다. 같은 커뮤니티에 속한 노드들끼리는 서로 다른 커뮤니티의 노드들보다 연결될 확률이 더 높습니다.

a-MMSBM’s Method

이 모델이 어떻게 두 노드 사이에 엣지를 생성하는지 상상해보면 이해하기 쉽습니다.

  1. 커뮤니티 선택: 엣지를 그릴지 결정할 두 노드(A, B)가 있습니다. 각 노드는 먼저 어떤 커뮤니티의 “모자”를 쓸지 자신의 소속 분포($\pi$)에 따라 확률적으로 선택합니다. 예를 들어, 노드 A는 ‘머신러닝’ 모자를, 노드 B는 ‘통계’ 모자를 쓸 수 있습니다.
  2. 연결 결정:
    • 만약 두 노드가 같은 커뮤니티 모자(예: 둘 다 ‘머신러닝’)를 썼다면, 해당 커뮤니티의 연결 강도($\beta_{머신러닝}$)라는 높은 확률로 엣지가 생성됩니다.
    • 만약 두 노드가 다른 모자를 썼다면, 커뮤니티와 무관한 매우 낮은 기본 확률($\delta$) 로 엣지가 생성됩니다.

BGCNN은 이 과정을 역으로 추적합니다. 즉, 관찰된 그래프($G_{obs}$)의 연결 상태를 보고, 각 노드가 어떤 커뮤니티 소속 분포($\pi$)를 가지며 각 커뮤니티가 얼마나 강하게 뭉쳐있는지($\beta$)를 추론하는 것입니다. 이렇게 학습된 파라미터들은 관찰된 그래프의 이면에 숨겨진 구조적 패턴을 담고 있습니다.

더보기: a-MMSBM의 알고리즘과 수학적 정의 --- Linking Algorithm 두 노드 $a, b$ 사이의 링크 $y_{ab}$를 생성하는 알고리즘은 다음과 같습니다. 1. 각 노드의 커뮤니티 소속 분포로부터 사용할 커뮤니티를 샘플링합니다: $z_{ab} \sim \pi_a$, $z_{ba} \sim \pi_b$ 2. 만약 두 노드가 같은 커뮤니티 $k$를 선택했다면 ($z_{ab} = z_{ba} = k$): - 해당 커뮤니티의 연결 강도 $\beta_k$에 따라 베르누이 분포에서 링크를 샘플링합니다: $y_{ab} \sim \text{Bernoulli}(\beta_k)$ 3. 만약 다른 커뮤니티를 선택했다면: - 매우 작은 교차 커뮤니티 확률 $\delta$에 따라 링크를 샘플링합니다: $y_{ab} \sim \text{Bernoulli}(\delta)$
Parameter Posterior 베이즈 정리에 따라, 관찰된 그래프 $G_{obs}$가 주어졌을 때 파라미터 $\pi$와 $\beta$의 결합 사후분포는 다음과 같이 표현됩니다. $$p(\pi, \beta|G_{obs}) \propto p(\beta)p(\pi)p(G_{obs}|\pi, \beta)$$ $$= \prod_{k=1}^{K} p(\beta_k) \prod_{a=1}^{N} p(\pi_a) \prod_{1 \leq a < b \leq N} \sum_{z_{ab}, z_{ba}} p(y_{ab}, z_{ab}, z_{ba}|\pi_a, \pi_b, \beta)$$ * 여기서 $p(\beta)$와 $p(\pi)$는 파라미터의 **사전분포(Prior)** 입니다. 논문에서는 커뮤니티 강도 $\beta_k$에 대해서는 **베타 분포($\text{Beta}(\eta)$)**, 노드의 커뮤니티 소속 분포 $\pi_a$에 대해서는 **디리클레 분포($\text{Dir}(\alpha)$)** 를 사용합니다. ($\eta$와 $\alpha$는 하이퍼파라미터)

4. Final Algorithm of BGCNN

지금까지 살펴본 모든 개념(사후확률, 몬테카를로 근사, a-MMSBM)을 종합한 최종 알고리즘의 흐름은 다음과 같습니다.

BGCNN step

INPUT: 관찰된 그래프 $G_{obs}$, 노드 특징 $X$, 알려진 레이블 $Y_L$ OUTPUT: 불확실성이 반영된 예측 확률 $p(Z |Y_L,X, G_{obs})$

  1. 초기화 (Initialization)
    • 효율적인 학습을 위해, 일반 GCN을 먼저 학습시켜 가중치($W$)와 MMSBM 파라미터($\pi, \beta$)의 합리적인 시작점을 찾습니다.

      “아무 값에서나 시작하는 게 아니라, 먼저 일반 GCN으로 어느 정도의 베이스라인을 잡아두는 과정입니다. 덕분에 전체 학습이 더 빠르고 안정적으로 수렴할 수 있습니다.”

  2. 외부 루프 시작: 그래프 샘플링 (for $i=1$ to $N_G$)
    • 그래프 구조의 불확실성을 포착하기 위해 $N_G$개의 다른 그래프를 샘플링하는 과정입니다.
    • a. MMSBM 추론: 관찰된 그래프 $G_{obs}$로부터 MMSBM 파라미터의 MAP 추정치($\hat{\pi}, \hat{\beta}$)를 계산합니다. 이 단계는 $G_{obs}$의 구조적 특징을 통계 모델 파라미터로 요약하는 과정입니다.
    • b. 그래프 샘플링: 추론된 파라미터($\hat{\pi}, \hat{\beta}$)를 사용하여 확률 모델 $p(G \hat{\pi},\hat{\beta})$로부터 새로운 “가상” 그래프 $G_i$를 샘플링합니다.
  3. 내부 루프 시작: 가중치 샘플링 (for $s=1$ to $S$)
    • 각각의 가상 그래프 $G_i$ 위에서, 모델 파라미터의 불확실성을 포착하기 위해 $S$개의 다른 가중치 세트를 샘플링합니다.
    • a. 가중치 샘플링: $G_i$를 입력으로 받은 GCN에서 MC Dropout을 사용하여 가중치 샘플 $W_{s,i}$를 얻고, 이를 통해 예측을 수행합니다.
  4. 최종 예측 집계 (Aggregation)
    • 총 $N_G \times S$번의 예측 결과를 모두 수집하여 평균을 냅니다. 이 평균값이 바로 그래프 구조와 모델 가중치의 불확실성을 모두 통합한 최종 예측 확률이 됩니다. \(p(Z|Y_L, X, G_{obs}) \approx \frac{1}{N_G S} \sum_{i=1}^{N_G} \sum_{s=1}^{S} p(Z|W_{s,i}, G_i, X)\)

Experimental Results

Dataset \& Setup

실험에는 논문 인용 네트워크 데이터셋인 Cora, Citeseer, Pubmed가 사용되었습니다. 하이퍼파라미터는 기존 GCN 연구의 표준 설정을 대부분 따랐으며, MC Dropout을 통해 베이지안 추론을 수행했습니다.

데이터셋 노드 수 엣지 수 특징 수 클래스 수
Cora 2,708 5,429 1,433 7
CiteSeer 3,327 4,732 3,703 6
Pubmed 19,717 44,338 500 3

Main Result

  • 적은 레이블에서 성능 향상: Cora와 Citeseer 데이터셋에서, 특히 학습에 사용되는 레이블이 클래스당 5개 또는 10개로 매우 적을 때 BGCNN은 기존 GCN보다 통계적으로 유의미하게 더 높은 분류 정확도를 보였습니다. 이는 그래프 구조의 불확실성을 모델링하는 것이 일종의 규제 효과를 주어 적은 데이터에서도 더 일반화된 학습을 가능하게 함을 시사합니다.

  • 모델 가정의 중요성: 반면, Pubmed 데이터셋에서는 레이블이 적을 때를 제외하고는 기존 방법보다 성능이 다소 낮았습니다. 논문은 Pubmed 그래프가 다른 데이터셋에 비해 커뮤니티 내의 연결 밀도가 훨씬 낮아, ‘같은 커뮤니티끼리 잘 뭉친다’는 a-MMSBM 모델의 가정이 잘 맞지 않았기 때문이라고 분석합니다. 이는 BGCNN의 성능이 그래프 생성 모델의 선택에 영향을 받을 수 있음을 보여줍니다.

New Insight

BGCNN의 가장 흥미로운 부분 중 하나는, 학습된 a-MMSBM 모델을 통해 그래프 자체에 대한 인사이트를 얻을 수 있다는 점입니다.

  • 노이즈 엣지 식별: 관찰된 엣지 중, 모델이 추정한 ‘연결될 확률’이 가장 낮은 엣지들은 대부분 서로 다른 커뮤니티(클래스)를 연결하는 엣지였습니다. 이는 해당 엣지들이 노이즈일 가능성이 높다는 것을 의미합니다.
  • 누락된 엣지 복원: 반대로, 관찰되지 않은 엣지 중 ‘연결될 확률’이 가장 높게 추정된 엣지들은 대부분 동일한 커뮤니티 내 노드들을 연결하는 엣지였습니다. 이는 모델이 데이터에 존재하지 않지만, 구조적으로 존재해야 할 가능성이 높은 링크를 성공적으로 찾아냈음을 의미합니다.

Reference

업데이트:

참고

Moran’s I Statistics

3 분 소요

이 포스팅은 공간통계에서 자주 사용하는 공간 자기상관에 대한 통계량 Moran’s I에 대해 설명하는 글입니다.