Bayesian Kernel Machine Regression (BKMR)
본 포스팅에서는 Bayesian Kernel Machine Regression (BKMR)의 이론적 배경을 정리하고 간단한 실습을 진행합니다.
Introduction
데이터 분석 및 모델링에서는 다수의 예측 변수(predictor)가 갖는 복잡한 비선형성, 상호작용, 그리고 예측 불확실성을 동시에 다루는 일이 자주 요구되며, 필수적입니다.
전통적인 선형 회귀 기법은 다음과 같은 한계를 지닙니다:
- 비선형 관계 포착의 어려움
변수와 결과 간에 임계점, 포화 구간, 급격한 변화 같은 패턴이 있을 때 직선 모델로는 설명하기 어렵습니다. - 상호작용 효과 식별의 한계
두 개 이상의 변수가 결합하여 비례 이상의 시너지나 길항 효과를 보일 때 이를 자동으로 탐지하기가 힘듭니다. - 변수 선택의 복잡성
다변량 환경에서 어떤 변수를 모델에 포함할지 결정하는 과정이 직관적이지 않습니다. - 불확실성 정량화 부족
예측값만 제공되고, 파라미터 추정의 불확실성(credible interval)을 함께 제시하지 않으면 신뢰도 있는 해석이 어렵습니다.
Bayesian Kernel Machine Regression(BKMR)은 이러한 단점을 통합적으로 해결하기 위해 설계된 베이지안 회귀 프레임워크입니다.
BKMR은 다변량 입력의 비선형·상호작용 효과를 유연하게 모델링하고, 변수 선택 및 사후분포 기반 불확실성 정량화를 동시에 제공할 수 있습니다.
- 다변수 통합 모델링
여러개의 변수를 하나의 커널 함수로 결합하여, 개별 및 혼합 효과를 일관되게 추정합니다. - 비선형·상호작용 효과 자동 학습
Gaussian Process 기반의 커널 사전분포를 사용해, 임계점(threshold)·정상화(plateau)·교호작용(interaction)을 유연하게 포착합니다. - Posterior Inclusion Probability(PIP)
변수 선택(variable selection)을 통해, 각 변수가 모델에 포함될 사후확률을 제공함으로써 중요 변수를 직관적으로 식별합니다. - 사후분포 기반 불확실성 정량화
MCMC 샘플링을 통해 얻은 사후분포로 예측값에 대한 95% credible interval을 산출하여, 결과 해석의 신뢰성을 높입니다.
BKMR Model
1. Hierarchical Model Specification
관측치 (i)에 대해
\[y_i = h(\mathbf{x}_i) + \mathbf{z}_i^\top \boldsymbol{\beta} + \epsilon_i,\quad \epsilon_i \sim \mathcal{N}(0, \sigma^2),\]여기서
- $\mathbf{x}_i\in\mathbb{R}^p$ : 주요 예측 변수
- $\mathbf{z}_i\in\mathbb{R}^q$ : 선형 고정효과 변수(예: 나이·성별)
- $\boldsymbol{\beta}\in\mathbb{R}^q$ : 고정효과 계수
- $h(\cdot)$ : 다변량 노출의 비선형·상호작용 효과를 담는 함수
- $\epsilon_i$ : 정규 오차
전체 데이터에 대해
\(\mathbf{h} = \bigl(h(\mathbf{x}_1),\dots,h(\mathbf{x}_n)\bigr)^\top\)
는 다음 Gaussian Process 사전분포를 따릅니다:
$\mathbf{K}_\theta$는 ${\mathbf{x}_i}$ 간 커널 행렬입니다.
2. Kernel Construction
커널 행렬 $\mathbf{K}_\theta \in\mathbb{R}^{n\times n}$의 원소:
\[\mathbf{K}_{\theta_{ij}} = K_\theta(\mathbf{x}_i, \mathbf{x}_j)\]대표적인 선택:
- RBF 커널
\(K_{\mathrm{RBF}}(\mathbf{x},\mathbf{x}') = \sigma_f^2 \exp\!\Bigl(-\tfrac12 (\mathbf{x}-\mathbf{x}')^\top \mathbf{L}^{-2} (\mathbf{x}-\mathbf{x}')\Bigr),\) $\mathbf{L}=\mathrm{diag}(\ell_1,\dots,\ell_p)$ - Matern 커널 $\nu=1.5$ 또는 $2.5$
\(K_{\nu}(r) = \sigma_f^2 \frac{2^{1-\nu}}{\Gamma(\nu)} \Bigl(\sqrt{2\nu}\tfrac{r}{\ell}\Bigr)^{\nu} K_{\nu}\Bigl(\sqrt{2\nu}\tfrac{r}{\ell}\Bigr),\quad r=\|\mathbf{x}-\mathbf{x}'\|.\)
3. Priors & Hyperpriors
- $\boldsymbol{\beta} \sim \mathcal{N}(\mathbf{0},\,\tau^2 \mathbf{I}_q)$
- $\sigma^2 \sim \mathrm{Inv}\text{-}\Gamma(a_0,b_0)$
- Scale/Bandwidth $\ell_j,\sigma_f \sim \mathrm{Half\text{-}Cauchy}(0,s)$
4. Likelihood & Posterior
우도: \(\mathbf{y}\mid \mathbf{h},\boldsymbol{\beta},\sigma^2 \;\sim\; \mathcal{N}\bigl(\mathbf{h} + \mathbf{Z}\boldsymbol{\beta},\,\sigma^2 \mathbf{I}_n\bigr).\)
사후분포: \(p(\mathbf{h}, \boldsymbol{\beta}, \sigma^2, \theta \mid \mathbf{y}) \;\propto\; p(\mathbf{y}\mid \mathbf{h},\boldsymbol{\beta},\sigma^2)\, p(\mathbf{h}\mid \theta)\,p(\boldsymbol{\beta})\,p(\sigma^2)\,p(\theta).\)
5. MCMC Sampling
- Gibbs 샘플링
- $\boldsymbol{\beta}\mid \cdots$ : 다변량 정규분포
- $\mathbf{h}\mid \cdots$ : 다변량 정규분포
- $\sigma^2\mid \cdots$ : Inverse-Gamma
- Metropolis–Hastings / Elliptical Slice
- 커널 파라미터 $\theta=(\ell_1,\dots,\ell_p,\sigma_f)$ 업데이트
- 진단
- Trace plot, $\hat{R}$, effective sample size(ESS)
MCMC Sampling 절차에 대한 자세한 설명은 MCMC Sampling 글을 참고하세요.
Lab
시뮬레이션 데이터를 생성하여 BKMR 모델을 적합하고, 결과를 요약·시각화해 보겠습니다.
library(bkmr) # devtools::install_github("jenfb/bkmr")
library(dplyr)
set.seed(123)
dat <- SimData(n = 80, M = 3) # n: 관측치 수, M: 노출 변수 개수
y <- dat$y
Z <- dat$Z # p차원 노출 변수 행렬
X <- dat$X # 보조 변수(예: 나이, 성별) 행렬
# BKMR 모델 적합
fitkm <- kmbayes(
y = y,
Z = Z,
X = X,
iter = 500,
varsel = TRUE,
verbose = FALSE
)
print(fitkm)
summary(fitkm)
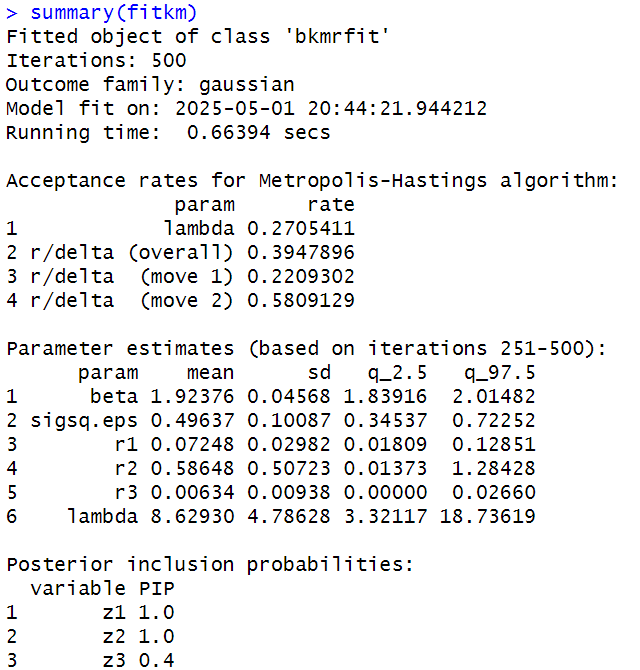
MCMC 500회 반복 후 산출된 주요 파라미터(β, σ², 커널 하이퍼파라미터) 추정치의 평균(mean), 표준편차(sd), 95% 사후분위수(q_2.5, q_97.5)와 각 노출 변수의 Posterior Inclusion Probability(PIP)를 보여줍니다.
다음의 PIP는 변수선택에 활용합니다. \(PIP = \dfrac{\text{\# of MCMC iterations in which variable j is included}}{\text{total MCMC iterations}}\)
# 변수 선택 지표(PIP) 추출 및 확인
pips <- ExtractPIPs(fitkm)
print(pips)
# 단일 변수 노출–반응 함수 계산
pred.univar <- PredictorResponseUnivar(
fit = fitkm,
method = "approx",
ngrid = 50,
q.fixed = 0.5
)
library(ggplot2)
ggplot(pred.univar, aes(x = z, y = est)) +
geom_ribbon(aes(ymin = est - 1.96 * se,
ymax = est + 1.96 * se),
alpha = 0.3) +
geom_line() +
facet_wrap(~ variable, scales = "free_x") +
labs(
x = "노출 변수 값 (z)",
y = "예측된 h(z)",
title = "단일 변수 노출–반응 함수"
) +
theme_minimal()
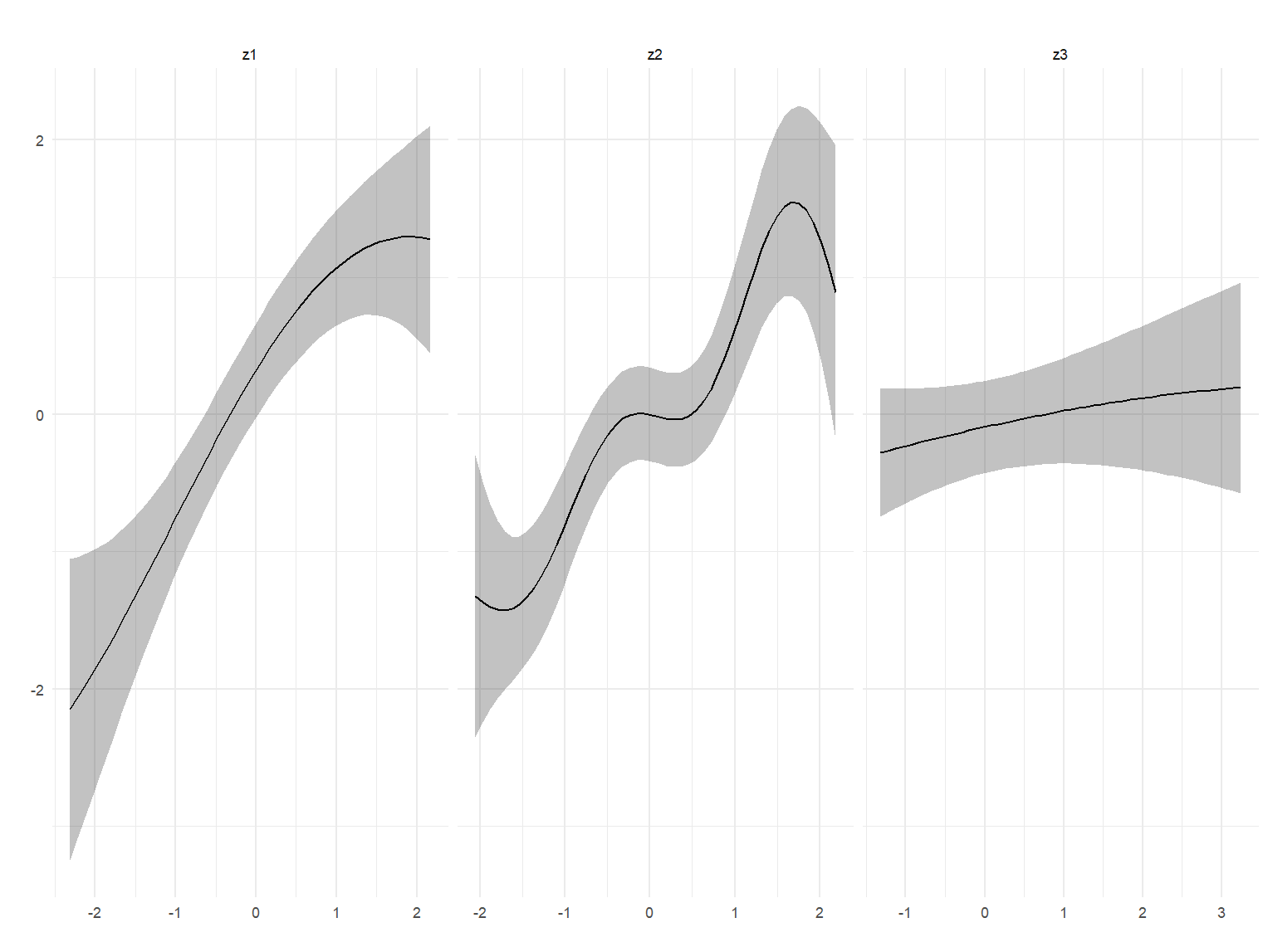
z1, z2, z3 세 변수 각각의 노출값(z)에 대한 함수 (h(z))의 중앙 추정치(검은 실선)와 95% 신뢰구간(회색 밴드)을 시각화했습니다.
각 패널은 개별 변수의 비선형 효과의 형태를 보여줍니다.
risks <- OverallRiskSummaries(
fit = fitkm,
qs = seq(0.25, 0.75, by = 0.1),
q.fixed = 0.5,
method = "approx"
)
print(risks)
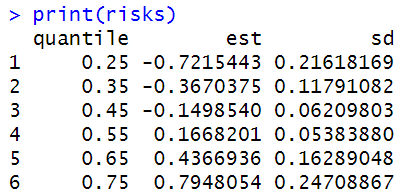
분위수(0.25, 0.35, 0.45, …, 0.75)에 따른 Risk 추정치(est)와 표준편차(sd)를 테이블 및 그래프로 나타냈습니다.
혼합물 효과가 특정 분위수 구간에서 어떻게 변화하는지 확인할 수 있습니다.
Conclusion
이번 포스팅에서는 Bayesian Kernel Machine Regression(BKMR)의 이론적 배경과 R 패키지 bkmr를 활용한 실습 예제를 살펴보았습니다. 요약하면
- 다변량 노출 변수를 하나의 커널 함수로 통합해, 복수의 예측 변수가 갖는 비선형성과 상호작용을 동시에 포착할 수 있습니다.
- Gaussian Process 기반 커널 사전분포를 통해 임계점이나 포화 구간 같은 복잡한 패턴을 유연하게 학습합니다.
- Posterior Inclusion Probability(PIP) 를 이용한 변수 선택 기능으로, 중요한 변수를 직관적으로 확인할 수 있습니다.
- MCMC 사후분포로부터 95% credible interval을 산출함으로써, 예측값의 불확실성까지 정량적으로 제시합니다.

댓글남기기