[Paper Review] Graph Attention Networks
이 포스팅은 Velickovic et al. (2018) 의 논문 Graph Attention Networks를 읽고 정리한 글입니다.
Why Attention?
기존의 GCN과 같은 그래프 합성곱 네트워크는 노드의 특징을 집계할 때, 이웃 노드에 대해서 동일한 가중치를 부여하거나, 노드의 차수에 기반한 고정된 가중치를 사용했습니다. 이는 나의 이웃이 나에게 같은 양의 중요도를 갖는 다고 가정하는 것과 같습니다. 하지만 실제 데이터는 노드 간의 중요도의 차이가 있을 수 있습니다.
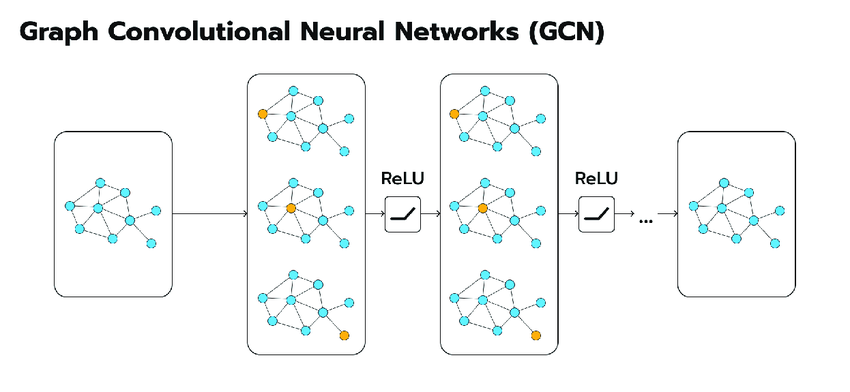
그래프 어텐션 네트워크(Graph Attention Networks, GAT) 는 이러한 한계를 극복하기 위해 제안되었습니다. GAT는 셀프 어텐션 메커니즘을 그래프에 적용하여, 모델이 학습과정에서 자기 자신을 포함한 이웃 노드간의 상대적 중요도를 계산하고 이를 가중치로 활용합니다. 이를 통해 더 유영하고 표현력 높은 노드 임베딩을 생성할 수 있습니다.
Model Architecture
각 GAT 레이어는 여러 단계의 연산을 통해 노드의 특징을 업데이트합니다. 아래 그림은 이 전체 과정을 요약해서 보여줍니다.
1. 선형 변환(Linear Transformation):
먼저 모든 노드에 공유되는 입력 특징 $h_i \in \mathbb{R}^F$에 대해 학습 파라미터 $W \in \mathbb{R}^{F’\times F}$ 를 곱해 $z_i = Wh_i$ 를 만듭니다.
- 해당 변환을 통해 모델은 특징을 더 표현력 높은 형태로 가공할 준비를 한다고 볼 수 있습니다.
- 여기서 $F$는 입력 특징의 차원, $F’$는 출력 특징의 차원입니다.
2. 어텐션 스코어 (Attention Score) 계산
다음으로, 노드 $i$와 그 이웃 노드 $j$ 사이의 어텐션 스코어 $e_{ij}$를 계산합니다. 이 스코어는 노드 $j$가 노드 $i$에게 얼마나 중요한지를 나타내는 정규화되지 않은 원시 점수입니다.
GAT의 핵심은 코사인 유사도나 내적(dot-product)처럼 고정된 규칙을 사용하는 대신, 유사도를 측정하는 방식 자체를 데이터로부터 학습한다는 점입니다. 이를 위해 단일 계층 피드포워드 신경망으로 구현된 어텐션 메커니즘 $a$를 사용합니다.
구체적인 계산 과정은, 먼저 두 노드의 변환된 특징 벡터 $Wh_i$와 $Wh_j$를 연결(concatenate)하고, 여기에 학습 가능한 가중치 벡터($\vec{\mathbf{a}}$)를 내적한 뒤, LeakyReLU 활성화 함수를 적용하는 방식입니다.
이를 하나의 수식으로 표현하면 다음과 같습니다.
\[e_{ij} = \text{LeakyReLU}\left(\vec{\mathbf{a}}^T [W h_i \mathbin{\|} W h_j]\right)\]3. 정규화(Normalization):
계산된 어텐션 계수 $e_{ij}$는 아직 모든 이웃에 대해 비교할 수 있는 형태가 아닙니다. 이를 위해 특정 노드 i의 모든 이웃 j에 대해 소프트맥스(Softmax) 함수를 적용하여 어텐션 가중치 $\alpha_{ij}$를 계산합니다.
\(\alpha_{ij} = \mathrm{softmax}_j\bigl(e_{ij}\bigr)
= \frac{\exp(e_{ij})}{\sum_{k\in\mathcal{N}(i)} \exp(e_{ik})}.\)
4. 특징 집계(Feature Aggregation):
마지막으로, 계산된 어텐션 가중치 $\alpha_{ij}$를 사용하여 이웃 노드들의 변환된 특징을 가중합(weighted sum)합니다. \(h_i' = \sigma\Bigl(\sum_{j\in\mathcal{N}(i)} \alpha_{ij} \, W h_j\Bigr).\)
- 이것이 GAT 레이어의 최종 출력입니다. 이 과정은 모든 노드에 대해 병렬적으로 수행됩니다.
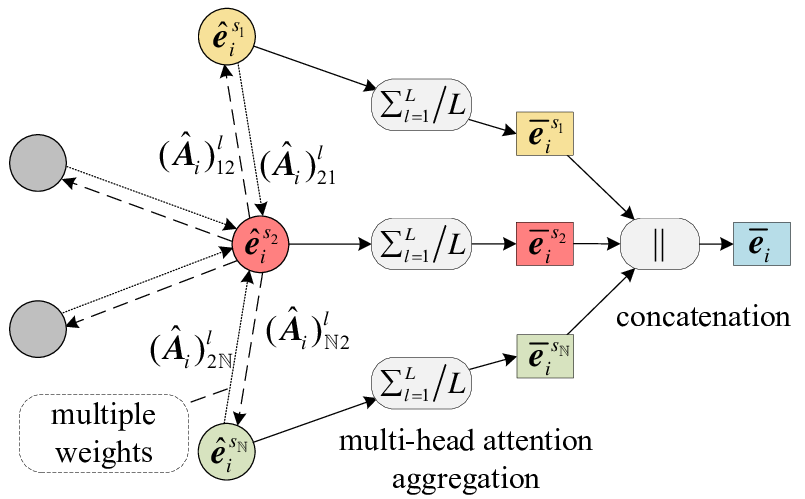
5. 멀티헤드 어텐션(Multi-Head Attention):
안정적인 학습과 풍부한 정보 추출을 위해 GAT는 멀티헤드 어텐션을 사용합니다. 이는 독립적인 어텐션 메커니즘($K$개)을 병렬적으로 수행한 후, 그 결과들을 하나로 합치는 방식입니다. 각 ‘헤드’는 서로 다른 가중치 행렬($W ^k$)과 어텐션 가중치를 가지며, 데이터의 서로 다른 측면에 집중하여 학습할 수 있습니다.
중간 레이어
-
$K$ 개의 헤드에서 나온 출력 특징을 Concatenate합니다.
\(h'_{i} = \underset{k=1}{\overset{K}{\Big\Vert}} \sigma\left(\sum_{j \in \mathcal{N}(i)} \alpha_{ij}^{k} W^{k} h_{j}\right)\)
- 여기서 “$\Vert$“는 Concatenate 연산을 의미합니다.
최종 레이어:
-
$K$개의 헤드에서 나온 출력 특징을 평균하여 최종 예측에 사용합니다.
\[h'_{i} = \sigma\left(\frac{1}{K} \sum_{k=1}^{K} \sum_{j \in \mathcal{N}(i)} \alpha_{ij}^{k} W^{k} h_{j}\right)\]
Pseudo-code
# H_in: 입력 노드 특징 행렬 (N x F_in)
# W: 학습 가능한 가중치 행렬 (F_out x F_in)
# a: 어텐션 메커니즘을 위한 가중치 벡터 (2 * F_out)
# 1. 선형 변환
H_transformed = H_in @ W.T # (N x F_out)
# 2. 어텐션 계수 계산 (모든 엣지에 대해)
# 엣지 (i, j)에 대해 H_transformed[i]와 H_transformed[j]를 연결
edge_features = concatenate(H_transformed[i], H_transformed[j])
e = LeakyReLU(edge_features @ a)
# 3. 정규화 (각 노드의 이웃에 대해 소프트맥스)
alpha = softmax(e, neighbors_of_each_node)
# 4. 특징 집계
H_out = sigma(alpha @ H_transformed) # 가중합
Reference
-
Velickovic, P. et al. (2018). Graph Attention Networks. International Conference on Learning Representations (ICLR). arXiv:1710.10903
-
[DMQA Open Seminar] Graph Attention Networks. YouTube. Link

댓글남기기