Gaussian Process(GP)

4 분 소요

이 포스팅은 Gaussian Process에 대한 개념을 소개하는 글입니다.

Introduction

Gaussian Process 는 함수 공간에 정의되며 시간이나 공간과 같은 연속적인 인덱스를 갖는 Stochastic Process(확률 과정)이며, 다음의 정의를 따릅니다.

\[f(x) \sim \mathcal{GP}(m(x), k(x,x'))\]

$m(x)$ : 평균함수
$k(x,x’)$ : 공분산 또는 커널 함수

Gaussian Process

위에서 보인 GP의 정의는 다음을 의미합니다:

임의의 유한한 입력 집합 ${x_1, x_2, \dots, x_n}$에 대해,
벡터 $\mathbf{f} = [f(x_1), f(x_2), \dots, f(x_n)]^\top$는 다음과 같은 다변량 정규분포를 따른다:

\[\mathbf{f} \sim \mathcal{N}(\mathbf{m}, K)\]

$\mathbf{m} = [m(x_1), \dots, m(x_n)]^\top$
$K_{ij} = k(x_i, x_j)$로 정의된 $n \times n$ 공분산 행렬

Example: GP prior

\[\begin{bmatrix} f(x_1) \\ f(x_2) \\ f(x_3) \end{bmatrix} \sim \mathcal{N} \left( \begin{bmatrix} m(x_1) \\ m(x_2) \\ m(x_3) \end{bmatrix}, \begin{bmatrix} k(x_1,x_1) & k(x_1,x_2) & k(x_1,x_3) \\ k(x_2,x_1) & k(x_2,x_2) & k(x_2,x_3) \\ k(x_3,x_1) & k(x_3,x_2) & k(x_3,x_3) \end{bmatrix} \right)\]

이러한 정의로 인해 GP는 함수 $f(x)$를 무한 차원의 정규분포로 간주할 수 있는 확률적 프레임워크를 제공합니다.

Contents of GP

1. Mean function

평균 함수는 각 입력 $x$에 대한 기댓값을 나타냅니다. 실제로는 centering을 통해 평균이 0인 GP를 주로 사용합니다.

2. Covariance(or Kernel) function

공분산 함수는 두 입력 $x$와 $x’$사이의 유사도를 측정합니다. 자주 사요오디는 커널함수로는 RBF(Radial Basis Function) 커널이 있으며 다음과 같이 정의됩니다.

$k(x, x’) = \sigma_f^2 \exp\left(-\frac{(x - x’)^2}{2\ell^2}\right)$

$\sigma_f^2$: 출력의 분산
$\ell$: 길이 척도 파라미터

이 커널은 입력 데이터 간의 거리가 가까울 수록 높은 유사도를 부여하여, 예측 함수의 부드러움을 조절합니다.

Gaussian Process Regression(GPR)

GP는 회귀 문제에 적용될 수 있습니다.
이는 함수 $f(x)$에 대한 prior를 GP로 설정하고, 관측 데이터를 통해 posterior를 추론하는 방식으로 이루어집니다.

Joint Distribution of Observed and Test Outputs

입력 $\mathbf{X} = [x_1, \dots, x_n]^\top$에 대한 관측값 $\mathbf{y}$와,
새로운 입력 $x_$에 대한 함수값 $f(x_)$의 조인트 분포는 다음과 같은 다변량 정규분포로 표현됩니다:

\[\begin{bmatrix} \mathbf{y} \\ f(x_*) \end{bmatrix} \sim \mathcal{N} \left( \begin{bmatrix} \mathbf{m} \\ m(x_*) \end{bmatrix}, \begin{bmatrix} K + \sigma_n^2 I & \mathbf{k}_* \\ \mathbf{k}_*^\top & k(x_*, x_*) \end{bmatrix} \right)\]

$K \in \mathbb{R}^{n \times n}$: 훈련 입력 간 커널 행렬
$\mathbf{k}* \in \mathbb{R}^n$: 테스트 입력 $x*$와 훈련 샘플 간 커널 벡터
$\sigma_n^2$: 관측 노이즈의 분산

Posterior Predictive Distribution

이 joint distribution으로부터, 조건부 정규분포의 공식을 이용해 $f(x_*) \mid \mathbf{X}, \mathbf{y}$의 분포는 다음과 같이 유도됩니다:

\[f(x_*) \mid \mathbf{X}, \mathbf{y} \sim \mathcal{N}(\mu(x_*), \sigma^2(x_*))\]

예측 평균:

\[\mu(x_*) = m(x_*) + \mathbf{k}_*^\top (K + \sigma_n^2 I)^{-1} (\mathbf{y} - \mathbf{m})\]

예측 분산:

\[\sigma^2(x_*) = k(x_*, x_*) - \mathbf{k}_*^\top (K + \sigma_n^2 I)^{-1} \mathbf{k}_*\]

Note: 위 식은 노이즈가 존재하는 현실적인 회귀 문제를 다루며, centering을 통해 $\mathbf{m} = \mathbf{0}$인 경우가 대부분입니다.

Interpretation of Predictive Variance

예측 분산 $\sigma^2(x_)$는 테스트 입력 $x_$에 대한 불확실성을 정량화합니다:

$\sigma^2(x_*)$가 작다 → 훈련 샘플들과 가까운 위치 → 신뢰 높은 예측
$\sigma^2(x_*)$가 크다 → 훈련 샘플이 없는 위치 → 높은 불확실성

이러한 정보는 예측 신용 구간(credible interval) 설정에 직접적으로 사용됩니다.

*Conditional Distribution of MVN

다변량 정규분포의 조건부 분포는 다음 공식을 따릅니다:

\[\begin{bmatrix} \mathbf{a} \\ \mathbf{b} \end{bmatrix} \sim \mathcal{N} \left( \begin{bmatrix} \mu_a \\ \mu_b \end{bmatrix}, \begin{bmatrix} \Sigma_{aa} & \Sigma_{ab} \\ \Sigma_{ba} & \Sigma_{bb} \end{bmatrix} \right) \quad \Rightarrow \quad \mathbf{b} \mid \mathbf{a} \sim \mathcal{N}(\mu_{b|a}, \Sigma_{b|a})\]

조건부 평균:

\[\mu_{b|a} = \mu_b + \Sigma_{ba} \Sigma_{aa}^{-1} (\mathbf{a} - \mu_a)\]

조건부 분산:

\[\Sigma_{b|a} = \Sigma_{bb} - \Sigma_{ba} \Sigma_{aa}^{-1} \Sigma_{ab}\]

이 공식을 그대로 GP의 예측 식 유도에 활용한 것입니다.

Visualization

아래 Plot는 Gaussian Process 회귀에서 posterior predictive distribution을 시각화한 것입니다:

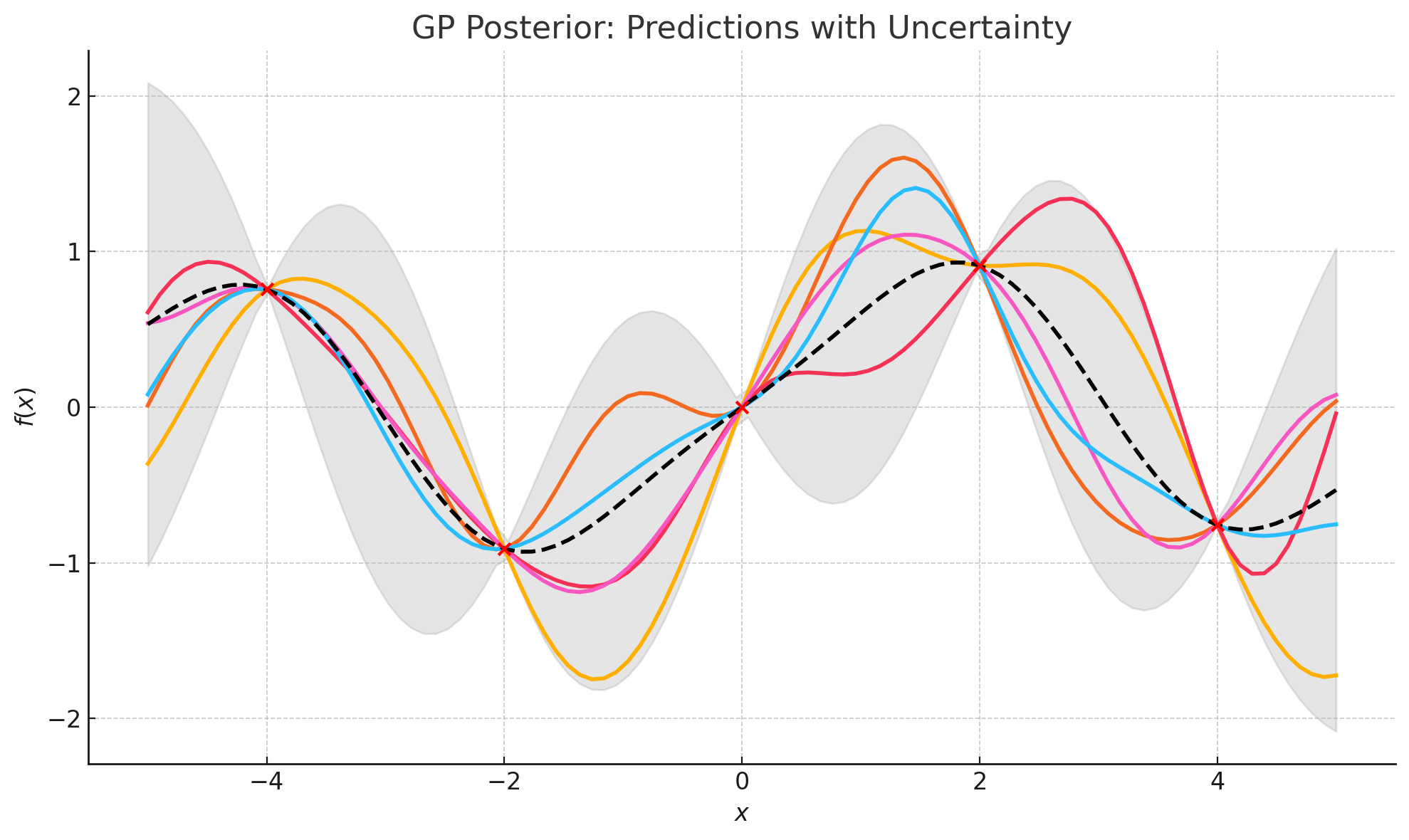
Posterior Prediction — Posterior predictive distribution 시각화

검정 점선: GP posterior의 예측 평균 $\mu(x_*)$입니다. 관측값을 부드럽게 통과하며, 가장 “가능성 높은 함수”를 나타냅니다. </br>
회색 음영 영역: 예측 신용 구간 95% 수준 $\mu(x_) \pm 1.96 \cdot \sigma(x_)$ → 이 영역은 모델이 얼마나 불확실한지를 나타냅니다. → 관측 데이터 근처에서는 좁고, 관측이 없는 영역에서는 넓어집니다. </br>
붉은 점들: 훈련 데이터 $(x_i, y_i)$. GP는 이 점들에 정확히 일치하도록 학습되며, 이 점들 주변에서 예측 분산이 거의 0에 수렴합니다. </br>
파란 실선들: GP posterior에서 샘플링한 함수들. 이들은 모두 같은 posterior 분포로부터 나온 것이며, 관측점 근처에서는 서로 일치하다가 멀어질수록 다양하게 퍼지는 모습을 보입니다.

GP는 단일 예측만 제공하지 않고, 함수의 분포 전체를 제공합니다.

이로 인해 “어디서 예측이 자신 있는지”, “어디서 불확실한지”를 한눈에 파악할 수 있습니다.

특히 회색 음영은 $\sigma^2(x_*)$ (예측 분산) 이 직관적으로 표현된 것이며, 이는 GP의 핵심 개념 중 하나입니다. —
code

시각화에 사용한 코드는 다음과 같습니다.

import numpy as np
import matplotlib.pyplot as plt

# 1. RBF 커널 함수 정의
def rbf_kernel(x1, x2, length_scale=1.0, sigma_f=1.0):
    sqdist = np.sum(x1**2, 1).reshape(-1, 1) + np.sum(x2**2, 1) - 2 * np.dot(x1, x2.T)
    return sigma_f**2 * np.exp(-0.5 / length_scale**2 * sqdist)

# 2. Posterior 계산 함수
def compute_gp_posterior(X_train, y_train, X_star, length_scale=1.0, sigma_f=1.0, sigma_n=1e-6):
    K = rbf_kernel(X_train, X_train, length_scale, sigma_f) + sigma_n**2 * np.eye(len(X_train))
    K_s = rbf_kernel(X_train, X_star, length_scale, sigma_f)
    K_ss = rbf_kernel(X_star, X_star, length_scale, sigma_f)
    
    K_inv = np.linalg.inv(K)
    mu_s = K_s.T @ K_inv @ y_train
    cov_s = K_ss - K_s.T @ K_inv @ K_s
    return mu_s.ravel(), cov_s

# 3. 데이터
X_train = np.array([[-4.0], [-2.0], [0.0], [2.0], [4.0]])
y_train = np.sin(X_train)

X_star = np.linspace(-5, 5, 100).reshape(-1, 1)

# 4. Posterior 계산
mu_post, cov_post = compute_gp_posterior(X_train, y_train, X_star)

# Poserior에서 샘플링
np.random.seed(42)
samples_post = np.random.multivariate_normal(mean=mu_post, cov=cov_post, size=5)

# 5. 시각화
plt.figure(figsize=(10, 6))
for i in range(5):
    plt.plot(X_star, samples_post[i], lw=2, color="C0")

# 평균 함수
plt.plot(X_star, mu_post, 'k--', lw=2) 

# 관측 데이터 포인트
plt.scatter(X_train, y_train, c='red', zorder=5) 

# 예측 분산을 반영한 95% 신용구간
plt.fill_between(
    X_star.ravel(),
    mu_post - 1.96 * np.sqrt(np.diag(cov_post)),
    mu_post + 1.96 * np.sqrt(np.diag(cov_post)),
    alpha=0.2,
    color="gray"
)

plt.title("GP Posterior: Predictions with Uncertainty", fontsize=14)
plt.xlabel("$x$", fontsize=12)
plt.ylabel("$f(x)$", fontsize=12)
plt.grid(True)
plt.tight_layout()
plt.show()

Conclusion

Gaussian Process는 함수 자체를 확률적 객체로 다루는 베이지안적 접근으로,
작은 데이터에서도 강력한 예측 성능과 불확실성 정량화를 제공합니다.

핵심 요약:

GP는 모든 입력 쌍에 대해 공분산 구조를 갖는 함수 prior
회귀 문제에서 joint Gaussian → conditional Gaussian을 통해 posterior 예측
커널 선택이 실전에서 중요한 역할을 함

Reference

X Facebook LinkedIn Bluesky

Junhee Kim