[Paper Review] Gaussian Processes Over Graphs
이 포스팅은 Venkitaraman et al. (2018) 의 논문 Gaussian Processes Over Graphs를 읽고 정리한 글입니다.
Introduction
그래프에 대한 개념은 Graph 글을 참고하세요.
전통적인 Gaussian Process(GP)는 입력 간의 유사도만을 반영해 함수값을 모델링하지만, 출력 벡터의 구조(예: 그래프 연결)에는 무관심합니다. 본 논문은 그래프 라플라시안을 GP prior에 결합함으로써, 노드 간 ‘매끄러움(smoothness)’ 제약을 추가한 GPG (Gaussian Processes on Graphs) 를 제안합니다.
- 문제: GP의 predictive variance가 소량·노이즈 데이터에서 과도하게 큼.
- 해결: 출력 노드 차원에서 $(I + \alpha L)^{-1}$ 스무딩 필터를 공분산에 삽입.
- 주장: GPG는 non‐trivial 그래프에서 항상 predictive variance를 줄이며, 실제 데이터에서도 성능 우수.
Background: Graph Signal Processing
Graph Laplacian
그래프 $G=(V,E)$에 대해 라플라시안 행렬 $L$ 은
\(L = D - A,\quad D_{ii}=\sum_j A_{ij}\)
이며,
\(y^\top L\,y = \sum_{(i,j)\in E}A_{ij}(y_i-y_j)^2\)
는 그래프 이차형식 또는 그래프 신호 $y$의 Dirichlet 에너지라고 부르며, 노드 값의 차이의 제곱합(매끄러움)의 척도가 됩니다. 이는 그래프 신호의 부드러움(Smoothness)을 정량화하는 핵심적인 지표로 자주 사용됩니다.
Graph Fourier & Smoothing Filter
라플라시안 고유분해 $L=V\Lambda V^\top$를 통해 주파수 성분을 분해하면,
\((I + \alpha L)^{-1} = V\,(I + \alpha\Lambda)^{-1}\,V^\top\)
로 저역(low-pass) 필터로 해석할 수 있습니다.
Methodology
1. Graph-Smoothing Prior
출력 벡터 $\mathbf{f}\in\mathbb R^M$에 대해
\(p(\mathbf{f})
\propto
\exp\Bigl(-\tfrac12\,\mathbf{f}^\top (I + \alpha L)\,\mathbf{f}\Bigr)
\quad\Longrightarrow\quad
\mathbf{f}\sim\mathcal N\bigl(0,\,(I+\alpha L)^{-1}\bigr).\)
2. GPG Covariance Function
Bayesian 선형 회귀 관점의 전통 GP:
\(K_{\rm GP}(x,x')
=\Phi(x)\,\tfrac1\alpha I\,\Phi(x')^\top.\)
GPG에서는 여기에 그래프 스무딩을 추가하여
\(\boxed{
K_{\rm GPG}(x,x')
= \Phi(x)\,(I+\alpha L)^{-1}\,\Phi(x')^\top
}\)
을 사용합니다.
- Toy 예제: $\Phi(x)=xI$ 로 두면 $K_{\rm GPG}(x,x’)=x\,x’\,(I+\alpha L)^{-1}$.
3. Variance Reduction Proof
GPG가 기존 GP보다 예측 분산을 줄이는 이유는 다음과 같습니다:
- PSD 순서 관계
- $L\succeq0$ 이므로 $I+\alpha L\succeq I$
- 양의 정부호 행렬의 역행렬은 순서를 반전: $(I+\alpha L)^{-1}\preceq I$
-
Prior 공분산 비교
\(K_{\rm GPG}(x,x') = \Phi(x)\,(I+\alpha L)^{-1}\,\Phi(x')^\top \preceq \Phi(x)\,I\,\Phi(x')^\top = \alpha\,K_{\rm GP}(x,x').\) - Predictive Covariance 부등식
GP의 predictive covariance는 $\Sigma_* = k_{} - k_^\top\,(K + \beta^{-1}I)^{-1}k_$ 입니다.
Prior 공분산 $K_{\rm GPG}\preceq K_{\rm GP}$ 이므로
\((K_{\rm GPG}+\beta^{-1}I)^{-1} \succeq (K_{\rm GP}+\beta^{-1}I)^{-1}, \quad k_*^{\rm GPG}\preceq k_*^{\rm GP}, \quad k_{**}^{\rm GPG}\preceq k_{**}^{\rm GP}.\)
이를 종합하면 \(\Sigma_*^{\rm GPG} \;\preceq\; \Sigma_*^{\rm GP},\) 즉 **예측 분산이 항상 감소함을 보장합니다.
4. Inference & Predictive Distribution
학습세트 ${x_i,\mathbf{t}i}{i=1}^N$에 대해
\(\begin{pmatrix} T \\ \mathbf{f}_* \end{pmatrix}
\sim
\mathcal N\!\Bigl(0,\,
\begin{pmatrix}
K + \beta^{-1}I & k_*\\
k_*^\top & k_{**}
\end{pmatrix}\Bigr),\)
\(\boxed{
\mathbf{f}_* \mid T
\sim
\mathcal N\bigl(\mu_*,\,\Sigma_*\bigr),
\quad
\mu_*=k_*^\top(C)^{-1}T,\;
\Sigma_*=k_{**}-k_*^\top(C)^{-1}k_*,
}\)
where $C=K+\beta^{-1}I$.
Experiments
Synthetic Graph Signal
# Define graph (chain of 5 nodes)
N = 5
A = np.zeros((N, N))
for i in range(N-1):
A[i, i+1] = A[i+1, i] = 1
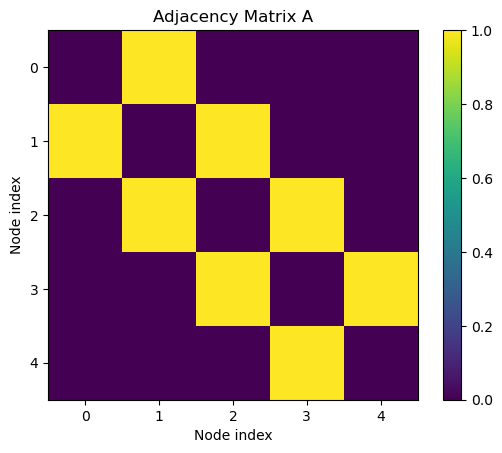
- 노드 간 연결 정보를 (0,1)로 표현한 행렬
D = np.diag(A.sum(axis=1))
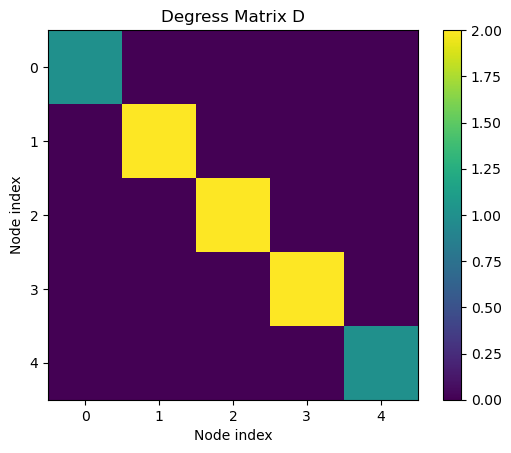
- 각 노드의 차수(각 노드에 연결된 노드의 수)를 표현한 행렬
L = D - A
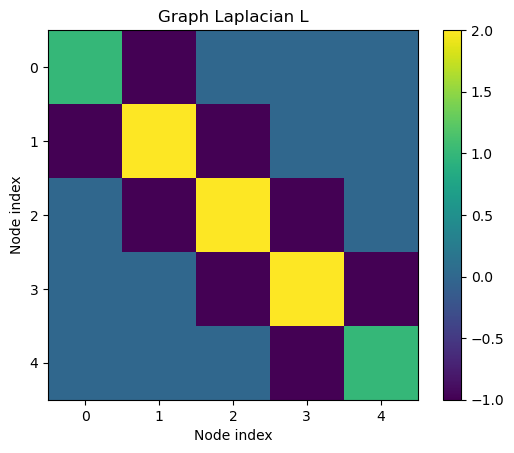
- D−A로 구성하여 이웃 간 차이를 측정한 행렬
# Graph smoothing filter
alpha = 1.0
F = np.linalg.inv(np.eye(N) + alpha * L)
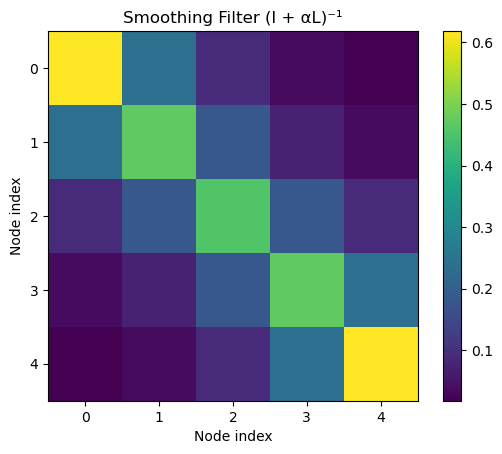
- Smoothing filter $F = (I + αL)^{-1}$.
- 저주파 성분을 강조합니다.
# Training inputs and outputs (example)
x_train = np.array([1.0, 2.0, 3.0])
y_train = np.array([
[1, 3, 2, 4, 3],
[2, 1, 3, 2, 4],
[3, 2, 1, 3, 5]
])
# Input kernel function
def k(x1, x2):
return x1 * x2
#Traditional GP covariance (3x3)
K_gp = np.array([[k(x1, x2) for x2 in x_train] for x1 in x_train])
beta_inv = 0.1
#Predictive variance for GP at x_star
x_star = 2.5
k_star = np.array([k(x, x_star) for x in x_train])
K_star_star = k(x_star, x_star)
C_gp = K_gp + beta_inv * np.eye(len(x_train))
var_gp = K_star_star - k_star.T @ np.linalg.inv(C_gp) @ k_star
var_gp_nodes = np.full(N, var_gp) # Same variance for all nodes
# GPG covariance via Kronecker
K_gpg = np.kron(K_gp, F)
k_star_blocks = np.vstack([k_star[i] * F for i in range(len(x_train))])
C_gpg = K_gpg + beta_inv * np.eye(N * len(x_train))
Var_gpg = K_star_star * F - k_star_blocks.T @ np.linalg.inv(C_gpg) @ k_star_blocks
var_gpg_nodes = np.diag(Var_gpg) # Variance per node

- 모든 노드에서 기존의 GP에 비해 예측분산이 줄어든 모습을 볼 수 있습니다.
Conclusion
“Gaussian Processes Over Graphs”는 그래프 라플라시안을 GP prior에 결합해 출력 노드 간 smoothness를 강제함으로써,
- 예측 분산을 수학적으로 항상 줄이고,
- 실험적으로 소량·노이즈 환경에서 RMSE 및 신뢰구간 성능을 크게 개선합니다.
기존의 GP와 제안된 GPG를 비교하여 요약하면 다음과 같습니다.
| 항목 | 전통 GP | 그래프 GP (GPG) |
|---|---|---|
| 출력 간 상관 | 독립 가정: $Cov(f_i(x),f_j(x’)) = k(x,x’)·δ_{ij}$ |
그래프 라플라시안 스무딩: $Cov(f(x),f(x’)) = Φ(x)·(I+αL)⁻¹·Φ(x’)ᵀ$ |
| 예측 불확실성 | 노드별 불확실성 분리 → 관측 적거나 노이즈 크면 개별 노드 불확실성 폭증 | “가상의 관측” 효과 → 이웃 노드 정보 전파로 예측 불확실성 감소 |
| 데이터 효율성 | 입력–출력 매핑 정보만 활용 → 출력 노드마다 별도 학습 필요 | 입력 정보 + 그래프 구조 정보 동시 활용 → 적은 관측으로도 안정적 예측 |
| 커널 수식 | $K_{GP}(x,x’) = Φ(x)·(1/α I)·Φ(x’)ᵀ$ | $K_{GPG}(x,x’) = Φ(x)·(I+αL)⁻¹·Φ(x’)ᵀ$ |

댓글남기기