Graph Basics
이 포스팅은 그래프 이론의 기본 개념—노드, 엣지, 인접행렬, 차수행렬, 라플라시안, 그래프 신호—을 정리한 글입니다.
What Is a Graph?
- 정의:
이산 객체들의 집합 $V$ 와, 그 객체들 사이의 관계를 나타내는 엣지 집합 $E$ 로 이루어진 구조
\(G = (V, E).\) - 노드(node, 정점): 데이터 포인트 하나. 예) 도시의 교차로, 소셜 네트워크의 사용자
- 엣지(edge, 간선): 노드 간의 연결. 예) 도로, 친구 관계
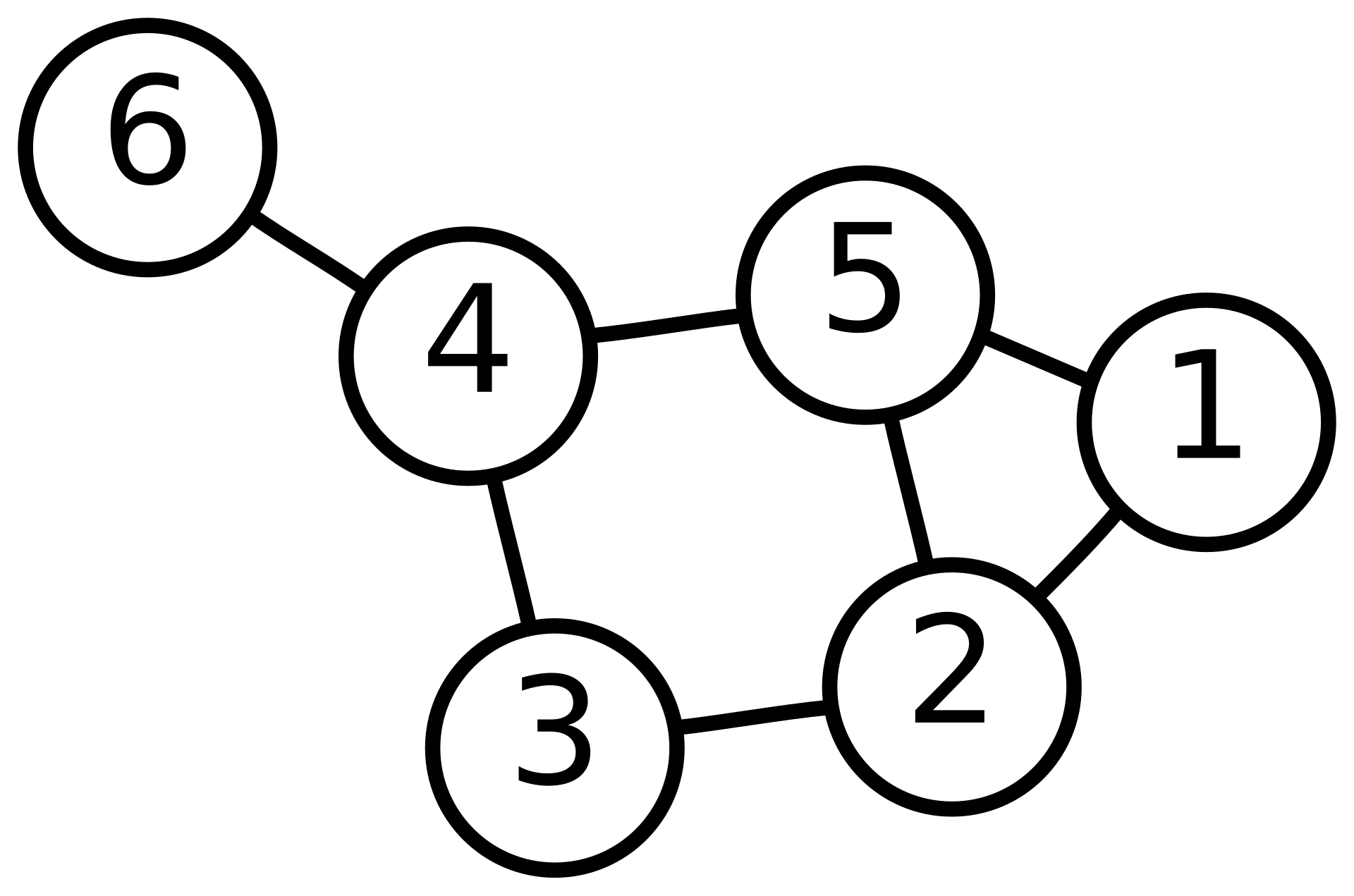
아래와 같은 간단한 그래프를 가정하고 진행하겠습니다.
Undirected vs. Directed
- 무향 그래프 (Undirected)
$(i,j)\in E$ 이면 $(j,i)$ 도 자동으로 포함. 대칭적 관계. - 유향 그래프 (Directed)
$(i \to j)$ 와 $(j \to i)$ 가 별개. 방향성 관계.
Unweighted vs. Weighted
- 단순 그래프(Simple, Unweighted):
연결 여부만 0/1 로 표현. - 가중치 그래프(Weighted):
엣지마다 실수 가중치 $w_{ij}$ 부여 → “연결 강도”를 나타냄.
Adjacency and Degree Matrices
Adjacency Matrix $A$
- 크기 $N\times N$.
- 비대각행렬
- 무향·단순 그래프:
\(A_{ij} = \begin{cases} 1, & (i,j)\in E,\\ 0, & \text{otherwise.} \end{cases}\) - 가중치 그래프: $A_{ij}=w_{ij}$.
\[A = \begin{pmatrix} 0 & 1 & 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \end{pmatrix}\]그래프 1 에서는 Adjacency Matrix가 다음과 같이 구성됩니다.
Degree Matrix $D$
- 대각행렬.
- $D_{ii} = \sum_{j=1}^N A_{ij}$ → 노드 $i$의 “차수”(연결 수).
\[D = \begin{pmatrix} 2 & 0 & 0 & 0 & 0 & 0 \\ 0 & 3 & 0 & 0 & 0 & 0 \\ 0 & 0 & 2 & 0 & 0 & 0 \\ 0 & 0 & 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0 & 3 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \end{pmatrix}\]Degree Matrix는 다음과 같이 구성됩니다.
Graph Laplacian
- 정의:
\(L = D - A.\) - 성질:
- Degree matrix와 Adjacency matrix를 차로 표현되지만, 두 행렬은 각각 대각, 비대각 행렬이기에 뺀다는 의미는 없고, 두 행렬을 하나로 합치는 효과가 존재합니다.
- 대칭적, PSD (모든 eigenvalue ≥ 0).
- 최소 eigenvalue $0$, 영고유벡터는 상수벡터.
- 의미:
\(y^\top L\,y = \sum_{(i,j)\in E}A_{ij}(y_i - y_j)^2.\) → “이웃 노드 간 값 차이”의 제곱합, 즉 매끄러움 측정.
\[L = D-A = \begin{pmatrix} 2 & -1 & 0 & 0 & 0 & 0 \\ -1 & 3 & -1 & 0 & -1 & 0 \\ 0 & -1 & 2 & -1 & 0 & 0 \\ 0 & 0 & -1 & 3 & -1 & -1 \\ -1 & -1 & 0 & -1 & 3 & 0 \\ 0 & 0 & 0 & -1 & 0 & 1 \end{pmatrix}\]Graph Laplacian은 다음과 같게 됩니다.
What Is a Graph Signal?
- 정의: 그래프의 각 노드 $i$ 위에 값(신호) $y_i$를 부여한 것.
- 벡터 표현: $y = [y_1,\dots,y_N]^\top \in \mathbb R^N$.
- 예시:
- 교차로별 차량 수
- 사용자별 활동 점수
- 센서별 온도
\[y = \begin{pmatrix} y_1 \\ y_2 \\ y_3 \\ y_4 \\ y_5 \\ y_6 \end{pmatrix} =(1,2,3,4,5,6)^\top\]Graph Signal $y_i$를 다음과 같이 가정해보겠습니다.
Graph Fourier Transform
- Eigen-decomposition:
\(L = V\,\Lambda\,V^\top,\quad \Lambda=\mathrm{diag}(\lambda_1,\dots,\lambda_N).\)Graph Laplacian을 Eigen-decomposition하면 다음의 결과가 도출됩니다.
\[V = \begin{pmatrix} 0.408 & 0.426 & 0.425 & 0.114 & -0.307 & 0.138 \\ 0.408 & 0.177 & -0.199 & -0.188 & 0.742 & -0.536 \\ 0.408 & -0.111 & -0.748 & 0.576 & -0.168 & 0.373 \\ 0.408 & -0.334 & -0.199 & -0.188 & -0.504 & -0.536 \\ 0.408 & 0.111 & 0.018 & -0.756 & 0.168 & 0.497 \\ 0.408 & 0.249 & 0.703 & 0.823 & -0.231 & -0.199 \end{pmatrix}\] \[\Lambda = \mathrm{diag}\bigl(0,\;0.586,\;2,\;3,\;3.414,\;4\bigr)\] -
Fourier Coefficients:
\(\hat y = V^\top\,y \;\approx\; \begin{pmatrix} 21 \\ -1 \\ -1 \\ -1 \\ -4 \\ -6 \end{pmatrix}\)
- 이는 원신호 $y$를 Graph fourier basis($L$의 Eigen-vector) 위에 투영했을 때 얻어지는 푸리에 계수입니다.
- $\hat{y}$는 “$y$를 $i$번째 고유벡터 $V_i$ 방향으로 얼마나 갖고 있는가?” 를 의미합니다.
- Interpretation:
- 작은 $\lambda_i$: 저주파(매끄러운 성분)
- 큰 $\lambda_i$: 고주파(급변 성분)
Graph Filtering
-
Low-pass Filter:
\(y_{\rm smooth} = V\,(I + \Lambda)^{-1}\,V^\top\,y \approx \begin{pmatrix}1.95 \\ 3.08 \\ 3.66 \\ 4.53 \\ 3.77 \\ 2.96\end{pmatrix}\) $\rightarrow$ 각 주파수 모드별로 필터 계수 $\dfrac{1}{1+\lambda_i}$를 곱해, 고유값이 작은(저주파) 성분은 1에 가까워져 더 살리고 고유값이 큰(고주파) 성분은 더 작아지게 되는 효과를 줍니다. 결과적으로 노드 신호 간 급격한 변화는 줄어들고 전반적으로 부드럽게 매핑됩니다. -
High-pass Filter:
\(y_{\rm high} = y - y_{\rm smooth} \approx \begin{pmatrix}-0.95 \\ -1.08 \\ -0.66 \\ -0.53 \\ 1.23 \\ 3.04\end{pmatrix}\) $\rightarrow$ 원본 신호에서 저주파 성분을 제거해, 이웃 간 값 차이가 큰 부분(고주파 성분)만 강조된 신호를 얻습니다. —
References
- Wikipedia. Graph theory. In Wikipedia, The Free Encyclopedia. Retrieved May 23, 2025, from https://en.wikipedia.org/wiki/Graph_theory

댓글남기기