Junhee Kim

I’m studying Bayesian ML, DL in Bayes Inference LAB, INHA University

8 분 소요

이 포스팅은 Papamakarios et al. (2021)의 “Normalizing Flows for Probabilistic Modeling and Inference”, Kobyzev et al. (2021)의 “Normalizing Flows: An Introduction and Review of Current Methods”, 그리고 Rezende & Mohamed (2015)의 “Variational Inference with Normalizing Flows” 논문을 읽고 정리한 글입니다.

Introduction

현대 기계학습의 가장 큰 과제 중 하나는 이미지, 음성, 텍스트와 같이 복잡하고 고차원적인 데이터의 확률 분포를 어떻게 모델링할 것인가입니다. VAEs, GANs, 그리고 최근의 Diffusion 모델과 같은 훌륭한 생성 모델들이 존재하지만, 이들은 대부분 새로운 데이터 포인트의 확률 밀도, 즉 가능도(likelihood)를 정확하게 계산할 수 없다는 근본적인 한계를 가집니다. 이는 모델 성능을 객관적으로 비교하거나, 이상 탐지를 수행하거나, 원칙에 입각한 통계적 추론을 적용하는 데 어려움을 야기합니다.

오늘 소개할 Normalizing Flows, (NF) 은 이러한 문제에 대한 강력한 해법을 제시합니다. 핵심 아이디어는 매우 직관적입니다.

다루기 쉬운 간단한 분포(예: 가우시안)를 연속적인 가역 미분 변환(invertible and differentiable transformations) 에 통과시켜, 우리가 원하는 복잡한 데이터 분포로 점진적으로 변형시키는 것.

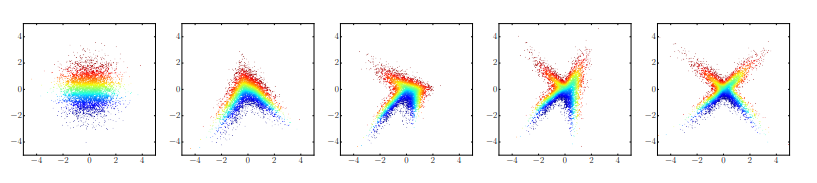
  4단계의 NF 변환 과정  
Figure 1: 4단계의 NF를 통해 표준 정규분포(왼쪽)가 점차 복잡한 십자 모양 분포(오른쪽)로 변환되는 과정. 각 단계는 간단한 변환이지만, 합성을 통해 매우 표현력 있는 모델을 만들 수 있다. (Papamakarios et al., 2021)

수식으로 표현하면, 간단한 분포의 변수 $u$를 변환 함수 $T$에 통과시켜 데이터 $x$를 생성하는 것입니다.

\[x = T(u), \;\; u \sim p_u(u)\]

이 구조의 가장 큰 장점은, 변환 과정이 아무리 복잡하더라도 데이터 $x$의 정확한 로그 확률을 계산할 수 있다는 점입니다. 바로 이 특징 덕분에, Normalizing Flow는 데이터 생성뿐만 아니라 변분 추론과 같은 다양한 추론 문제에까지 폭넓게 적용됩니다.

1. Mathematical Foundation of NF

NF 모델은 기본 분포(base distribution) 와 이를 변형시키는 가역 변환 함수(invertible transformation) 로 이루어집니다.

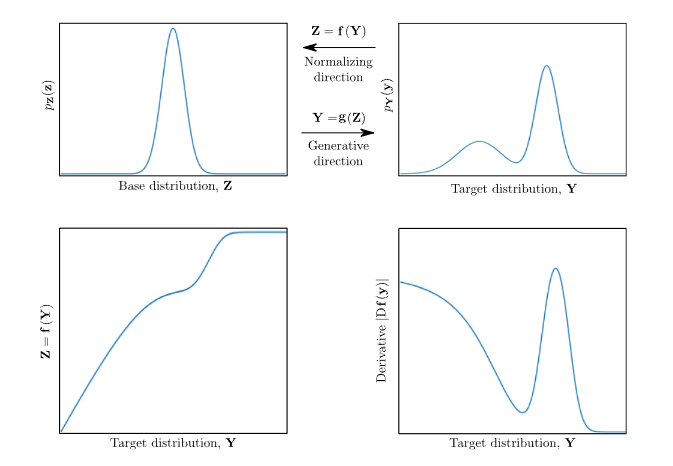
  정규화 흐름의 기본 원리  
Figure 2: 정규화 흐름의 기본 원리. Generative direction은 간단한 기본 분포 Z를 복잡한 목표 분포 Y로 변환한다. 반대로 Normalizing direction은 Y를 Z로 되돌리며, 이 역변환 f와 그 야코비안을 이용해 Y의 확률 밀도를 계산한다. (Kobyzev et al., 2021)


1.1 The Change of Variables Formula

NF가 정확한 확률 계산을 할 수 있게 해주는 수학적 원리는 바로 변수 변환 공식입니다. 기본 분포 공간의 변수 $u \in \mathbb{R}^D$와 데이터 공간의 변수 $x \in \mathbb{R}^D$ 사이에 가역 미분 변환(diffeomorphism) $T: u \mapsto x$가 존재할 때, $x$의 확률 밀도 함수 $p_x(x)$는 다음과 같이 계산됩니다.

</br>

\[p_x(x) = p_u(T^{-1}(x)) \left| \det J_{T^{-1}}(x) \right|\]

</br>

  • $p_u(\cdot)$: 우리가 잘 알고있는 간단한 기본 분포(주로 $\mathcal{N}(0, I)$)의 확률 밀도 함수입니다.
  • $T^{-1}(x)$: 변환 $T$의 역함수입니다. 데이터 $x$가 기본 공간의 어떤 $u$에서 기원했는지 역추적하는 함수입니다.
  • $ \det J_{T^{-1}}(x) $: 야코비 행렬식의 절댓값입니다. 변환 과정에서 발생한 부피의 변화율을 나타냅니다. 공간이 2배로 팽창했다면, 확률 밀도는 보존을 위해 1/2로 줄어들어야 합니다. 이 보정항 덕분에 변환 후에도 전체 확률의 합이 1로 유지(normalize)됩니다.

</br>

실제로는 여러 개의 간단한 변환 $T_k$를 합성($T = T_K \circ \dots \circ T_1$)하여 복잡한 변환을 만듭니다. 이 경우 로그 확률은 각 변환의 로그 행렬식의 합으로 표현됩니다.

</br>

\[\log p_x(x) = \log p_u(u) + \sum_{k=1}^K \log \left| \det J_{T_k^{-1}}(z_k) \right|, \\\textbf{where,}\;\; z_k = T_k(z_{k-1}),\;\; z_0 = u, z_K = x\]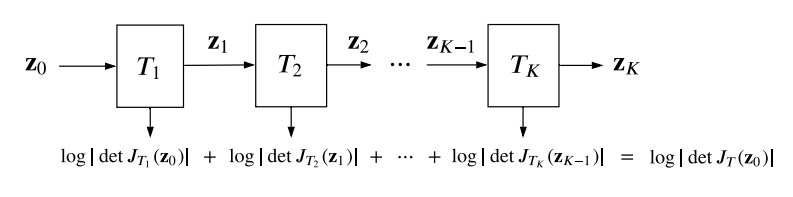
  K개의 변환으로 구성된 정규화 흐름  
Figure 3: K개의 변환으로 구성된 정규화 흐름의 구조. 전체 변환의 로그 야코비 행렬식은 각 개별 변환의 로그 야코비 행렬식의 합으로 간단하게 계산된다. (Papamakarios et al., 2021)

</br>

1.2 Expressive Power and Universality

이론적으로 NF는 적절한 조건 하에서 어떠한 목표 분포라도 원하는 정밀도로 근사할 수 있다는 것이 증명되었습니다. 즉, NF는 표현력에 한계가 없는 보편적 근사자(Universal Approximator) 입니다.

Proof: NF’s Universality

Papamakarios et al. (2021)에 제시된 증명

  1.  목표: 임의의 분포 $p_x(x)$를 간단한 균등분포(Uniform) $p_z(z)$로 변환하는 가역 함수 $F$가 존재함을 보이면 됩니다. (균등분포는 다시 가우시안 등으로 변환 가능하므로 이것으로 충분합니다).

  2.  확률의 연쇄 법칙: 먼저, 목표 분포 $p_x(x)$를 조건부 확률의 곱으로 분해합니다.     \(p_x(x) = \prod_{i=1}^D p_x(x_i | x_{<i})\)

  3.  변환 함수 F의 구성: 변환 $F: x \mapsto z$의 각 차원 $z_i$를, $x_i$의 조건부 누적분포함수(Conditional CDF) 로 정의합니다.     \(z_i = F_i(x_i, x_{<i}) = \int_{-\infty}^{x_i} p_x(x'_i | x_{<i}) dx'_i\)

  4.  가역성 및 야코비 행렬:     -   CDF는 단조 증가 함수이므로, 각 $F_i$는 $x_i$에 대해 가역적입니다. 또한 $z_i$는 $x_{>i}$에 의존하지 않으므로, 전체 함수 $F$의 야코비 행렬 $J_F(x)$는 하삼각행렬(lower-triangular matrix) 이 됩니다.     -   삼각행렬의 행렬식은 대각 원소의 곱입니다. 미적분학의 기본 정리에 의해 대각 원소는 $\frac{\partial F_i}{\partial x_i} = p_x(x_i | x_{<i})$가 됩니다.     -   따라서 야코비 행렬식은 다음과 같습니다.         \(\det J_F(x) = \prod_{i=1}^D \frac{\partial F_i}{\partial x_i} = \prod_{i=1}^D p_x(x_i | x_{<i}) = p_x(x)\)

  5.  최종 분포: 변수 변환 공식을 적용하면 $z$의 분포 $p_z(z)$는 다음과 같습니다.     \(p_z(z) = p_x(F^{-1}(z)) |\det J_{F^{-1}}(z)| = p_x(x) \cdot \frac{1}{|\det J_F(x)|} = p_x(x) \cdot \frac{1}{p_x(x)} = 1\)     이는 $z$가 균등분포를 따름을 의미합니다. 따라서 어떤 분포 $p_x(x)$든 균등분포로 변환하는 흐름이 항상 존재하며, 이는 NF의 보편성을 증명합니다.


2. Architectures of NF

NF 연구의 역사는 “가역적이면서 야코비안 행렬식 계산이 쉬운” 변환 함수 T를 어떻게 효율적으로 설계할 것인가에 대한 고민의 역사와 같습니다. 다양한 아키텍처들은 ‘표현력’과 ‘계산 효율성’ 사이의 트레이드오프 관계 속에서 각기 다른 철학적 선택을 나타냅니다.

2.1 Autoregressive Flows

  • 설계 철학: “강력한 구조적 제약으로 계산 효율성을 극대화한다.”
  • 핵심 원리: 출력의 각 차원 $y_t$가 이전 차원들 $x_{1:t-1}$에만 의존하도록 강력한 구조적 제약을 가합니다. \(y_t = h(x_t; \Theta_t(x_{1:t-1}))\) 이 제약 덕분에 야코비 행렬은 필연적으로 삼각행렬이 되고, 그 행렬식은 $O(D)$의 매우 빠른 시간에 계산 가능해집니다.
  • 구현과 트레이드오프:
    • 마스킹(Masking) 기반 (MAF/IAF): 신경망의 연결 일부를 마스킹하여 자기회귀 속성을 강제합니다. 하지만 이 구조는 계산 방향의 비대칭성을 낳습니다. MAF는 확률 계산이 빠른 대신 샘플링이 느리고, IAF는 그 반대입니다.
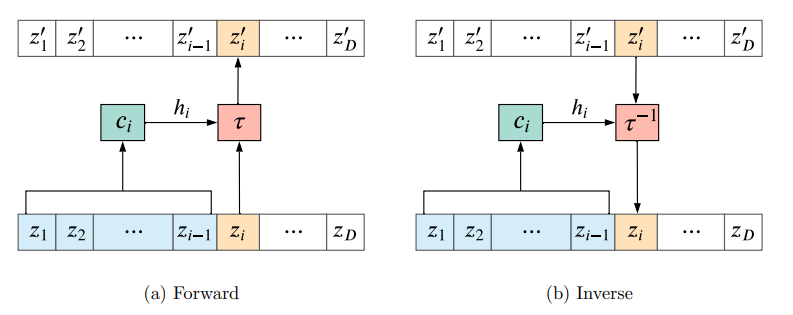
      자기회귀 흐름의 계산 과정  
    Figure 4: 자기회귀 흐름의 계산 과정. (a) 순방향(확률 계산)에서는 모든 입력 $z_i$가 병렬적으로 처리될 수 있다. (b) 역방향(샘플링)에서는 $z_i$를 계산하기 위해 이전 결과물 $z_{<i}$가 필요하므로 계산이 순차적으로 진행된다. (Papamakarios et al., 2021)
    • 결합 레이어 (Coupling Layers): 이 비대칭성 문제를 해결하기 위한 실용적 타협안입니다. 입력 $x$를 두 부분 $x^A, x^B$로 나누고, 한쪽은 그대로 둔 채 다른 쪽만 변환합니다. \(y^A = h(x^A; \Theta(x^B)), \quad y^B = x^B\) 이 구조는 양방향 계산 모두를 빠르게 만들어, NICE, RealNVP, Glow와 같은 모델들의 핵심 아키텍처로 자리 잡았습니다.
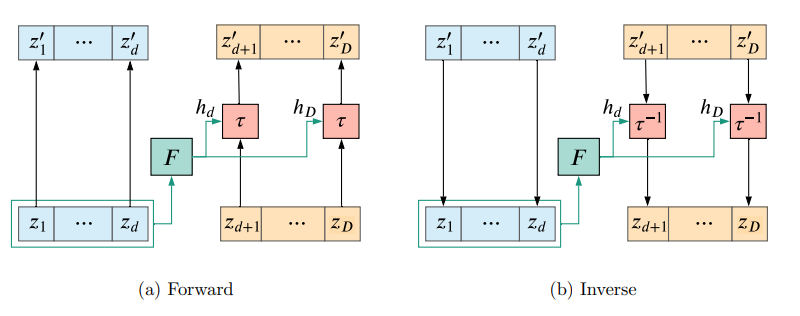
      결합 레이어의 구조  
    Figure 5: 결합 레이어(Coupling Layer)의 구조. 입력 벡터를 둘로 나눈 뒤, 한 부분($z_{1...d}$)을 이용해 다른 부분($z_{d+1...D}$)을 변환할 파라미터를 계산한다. 이 구조 덕분에 순방향과 역방향 계산이 모두 효율적이다. (Papamakarios et al., 2021)


2.2 Linear Flows

  • 설계 철학: “표현력은 낮지만, 정보 혼합을 위한 필수적인 유틸리티.”
  • 핵심 원리: $y = Wx$ 형태의 간단한 선형 변환입니다. 선형 흐름 자체의 표현력은 제한적이지만(가우시안을 가우시안으로 변환), 자기회귀 흐름과 같은 다른 층들 사이에 위치하여 변수들의 정보를 섞어주는(mixing) 필수적인 역할을 합니다. 특히 결합 레이어는 선형 흐름 없이는 일부 차원이 전혀 변환되지 않는 문제가 발생할 수 있습니다.
  • 구현과 트레이드오프:
    • 문제: 일반 행렬 $W$는 역행렬과 행렬식 계산 비용이 $O(D^3)$으로 매우 높습니다.
    • 해결책: 계산이 효율적인 행렬 분해(matrix decomposition)를 사용합니다.
      • PLU 분해: Glow에서 사용된 방식으로, 행렬을 순열(P), 하삼각(L), 상삼각(U) 행렬의 곱으로 표현하여 계산 효율을 높입니다.
      • QR 분해: 직교행렬(Q)과 삼각행렬(R)의 곱으로 표현하는 방식도 있습니다.


2.3 Residual & Continuous Flows

  • 설계 철학: “구조적 제약을 최소화하여 표현력을 극대화한다.”
  • 핵심 원리: 자기회귀 구조와 달리, 모든 차원이 서로 자유롭게 상호작용할 수 있는 유연한 구조에서 시작합니다.
    • 잔차 흐름: ResNet과 유사한 $y = x + F(x)$ 구조를 사용합니다.
    • 연속 시간 흐름: 변환을 상미분방정식(ODE) $\frac{dz_t}{dt} = F(z_t, t)$의 해로 정의합니다.
  • 새로운 트레이드오프: 이러한 유연성은 비싼 대가를 치릅니다.
    • 역변환: 더 이상 해석적으로 구할 수 없고, 반복적인 수치해석 알고리즘으로만 근사적으로 찾을 수 있습니다.
    • 야코비 행렬식: 정확한 계산이 불가능해져, 확률적 추정치(stochastic estimate) 를 사용해야 합니다. 이는 훈련 과정에서 로그 가능도에 노이즈가 낀 신호를 사용하게 된다는 근본적인 차이를 만듭니다.


2.4 고급 아키텍처: 단절된 분포 모델링

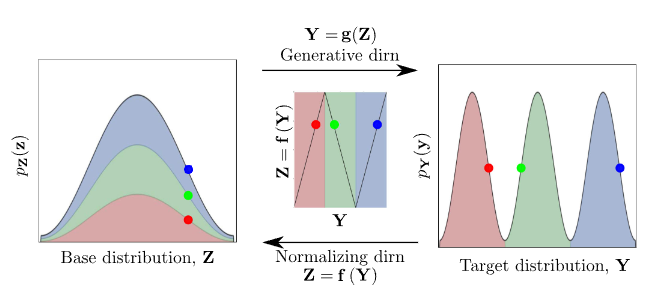
단일 연결된 분포로 표현하기 어려운, 여러 개로 단절된 모드를 가진 분포를 효과적으로 모델링하기 위한 구조도 제안되었습니다. 조각적 가역(Piecewise-Bijective) 함수를 이용하여, 목표 분포의 각기 다른 모드(영역)들을 각각 별개의 함수에 의해 기본 분포의 다른 영역으로 매핑합니다.

  조각적 가역 흐름의 원리  
Figure 6: 조각적 가역(Piecewise-Bijective) 함수의 원리. 목표 분포(오른쪽)의 각기 다른 모드(색깔로 구분)들이 각각 별개의 단조 함수(중앙)에 의해 기본 분포(왼쪽)의 다른 영역으로 매핑된다. (Kobyzev et al., 2021)

3. Training \& Application

3.1 Train: Maximizing Likelihood

NF는 데이터의 로그 확률 $\log p(x)$를 정확히 계산할 수 있기 때문에, 주로 최대 가능도 추정(MLE) 을 통해 직접적으로 학습됩니다. \(\mathcal{L}(\theta) = -\frac{1}{N} \sum_{n=1}^{N} \log p(x_n; \theta)\)

3.2 Application 1: Generative Modeling

정규화 흐름의 가장 직관적이고 널리 알려진 응용 분야는 바로 Generative Modeling 입니다. 이 모델들은 이미지(Glow), 음성(WaveGlow), 비디오(VideoFlow) 등 다양한 분야에서 데이터를 생성하는 데 성공적으로 활용되고 있습니다.

데이터 생성이 가능한 원리는 정규화 흐름의 가역적(invertible) 성질을 이용하는 것입니다. 학습과정이 데이터 공간에서 기본 공간으로 향하는 정규화 방향(Normalizing Direction, $u = T^{-1}(x)$) 을 사용했다면, 생성은 그 정반대의 과정을 따릅니다.

생성 과정은 다음과 같은 간단한 3단계로 이루어집니다:

  1. 기본 분포에서 샘플링 (Sample from Base Distribution)
    • 먼저, 간단하고 다루기 쉬운 기본 분포 $p_u(u)$ (예: 다변수 표준 정규분포 $\mathcal{N}(0, I)$)로부터 랜덤 벡터 $u$를 샘플링합니다. 이 과정은 매우 간단하고 비용이 저렴합니다.
  2. 생성 방향으로 변환 (Transform via Generative Direction)
    • 샘플링된 벡터 $u$를, 학습된 정규화 흐름의 생성 방향(Generative Direction), 즉 역변환의 역함수인 $T$에 통과시킵니다. \(x = T(u) = T_K \circ \dots \circ T_1(u)\)
    • 이 과정은 기본 공간의 단순한 점을, 모델이 학습한 복잡한 데이터 공간의 한 점으로 매핑하는 과정입니다.
  3. 최종 샘플 획득 (Obtain Final Sample)
    • 최종적으로 출력된 $x$가 바로 우리의 새로운 데이터 샘플입니다. 모델이 잘 학습되었다면, 이 샘플은 실제 데이터와 매우 유사한 특성을 갖게 됩니다.

이때, 생성 속도는 아키텍처에 따라 달라집니다.


3.3 Application 2: Probabilistic Inference (feat. Rezende & Mohamed, 2015)

NF의 진정한 힘은 복잡한 추론 문제에서 드러납니다. 특히 변분 추론(Variational Inference, VI) 과의 결합이 중요합니다.

  • VI의 문제점: 전통적인 VI는 다루기 힘든 사후 분포 $p(z x)$를 너무 단순한 분포(예: 가우시안) $q(z)$로 근사하여 정확도에 한계가 있었습니다.
  • NF의 역할: 이 근사 분포 $q(z)$ 자체를 정규화 흐름으로 만드는 것입니다. Rezende & Mohamed (2015)가 제안한 이 아이디어는 VI의 근본적인 한계를 돌파했습니다.

    Proof: VI와 NF의 결합

    1.  VI의 목적 함수는 증거 하한(ELBO), $\mathcal{L}$을 최대화하는 것입니다.     \(\mathcal{L} = \mathbb{E}_{q(z|x)}[\log p(x,z)] - \mathbb{E}_{q(z|x)}[\log q(z|x)]\)

    2.  여기서 근사 분포 $q(z x)$를 길이가 K인 NF로 정의합니다($z_K = T(z_0)$). $q_K(z_K x)$의 로그 확률은 다음과 같습니다.    
          $$\log q_K(z_K x) = \log q_0(z_0 x) - \sum_{k=1}^K \log\left \det \frac{\partial T_k}{\partial z_{k-1}}\right $$
    3.  이 식을 ELBO에 대입하고 기댓값을 초기 분포 $q_0$에 대한 것으로 바꾸면 다음과 같은 최종 목적 함수를 얻습니다.     \(\mathcal{L} = \mathbb{E}_{q_0(z_0|x)} \left[ \log p(x, z_K) - \log q_0(z_0|x) + \sum_{k=1}^K \log\left|\det \frac{\partial T_k}{\partial z_{k-1}}\right| \right]\)

Conclusion

이번 포스팅에서는 세 편의 핵심 논문을 바탕으로 Normalizing Flows의 이론적인 기초부터 다양한 아키텍처의 설계, 그리고 실제 활용 사례까지 살펴보았습니다. 긴 글 읽어주셔서 감사합니다.

Reference

업데이트:

참고

Moran’s I Statistics

3 분 소요

이 포스팅은 공간통계에서 자주 사용하는 공간 자기상관에 대한 통계량 Moran’s I에 대해 설명하는 글입니다.