PyMC를 이용한 확률적 프로그래밍 입문

5 분 소요

Introduction

이 포스팅은 파이썬 라이브러리 PyMC에 대한 예제를 다루겠습니다. 기본적인 개념을 쉽고 직관적으로 설명해보려고 합니다.

마케팅에서 흔히 볼 수 있는 A/B 테스트 문제를 모델링 해보려고 합니다.

실험 상황: 두 개의 랜딩 페이지

우리는 A와 B 두 가지 버전의 랜딩 페이지를 만들고 각각 1,000명의 방문자에게 노출시켰습니다.

A 페이지 : 1,000명 중 120명이 구매
B 페이지 : 1,000명 중 150명이 구매

이런 상황에서 “B 페이지의 전환율(Conversion Rate)이 더 높다!”고 단순하게 결론내릴 수 있지만, 과연 이 차이가 우연이 아닐까? 라는 의문을 품어봅시다. 베이지안 추론은 이 질문에 답을 줄 수 있습니다.

PyMC 모델링

1. 사전지식이 없는 경우

먼저, 우리가 A/B 테스트에 대해 아무런 정보가 없다고 가정하고, 오직 데이터에만 의존해 결론을 내려보겠습니다.

이런 상황에서는 우리의 초기 믿음을 사전 분포(Prior) 로, 실제 관측된 데이터를 우도 함수(Likelihood) 로 설정합니다. 이를 위해 각각에 적합한 확률분포를 선택해야 합니다.

사전 분포에는 베타 분포(Beta Distribution) 를 사용합니다. 이 분포는 0과 1 사이의 값만 가질 수 있어, 전환율처럼 확률을 모델링하는 데 적절합니다.

우도 함수에는 이항분포(Binomial Distribution) 를 사용합니다. 이 분포는 ‘정해진 횟수의 시도(총 방문자)’에서 ‘성공이 몇 번 일어났는지(전환 수)’를 모델링하는 데 가장 적합하기 때문입니다.

이제 이 개념들을 코드로 옮겨보겠습니다.

# 필요한 라이브러리와 데이터 정의
import pymc as pm
import arviz as az
import matplotlib.pyplot as plt

trials = 1000
conversions_a = 120
conversions_b = 150

# PyMC 모델 생성
with pm.Model() as uninformative_ab_test:
    # 사전 분포(Prior)에 아무런 정보가 없다고 가정
    # Beta(1, 1)은 0~1 사이 모든 값에 동일한 확률을 주는 분포
    p_A = pm.Beta("p_A", alpha=1, beta=1)
    p_B = pm.Beta("p_B", alpha=1, beta=1)

    # 우도 함수(Likelihood)는 데이터에 따라 이항 분포로 정의
    y_A = pm.Binomial("y_A", n=trials, p=p_A, observed=conversions_a)
    y_B = pm.Binomial("y_B", n=trials, p=p_B, observed=conversions_b)

    # 두 페이지의 전환율 차이 계산
    diff = pm.Deterministic("diff", p_B - p_A)

    # MCMC 샘플링을 통한 사후 분포(Posterior) 추론
    trace_uninformative = pm.sample(2000, tune=1000, cores=1, random_seed=42)

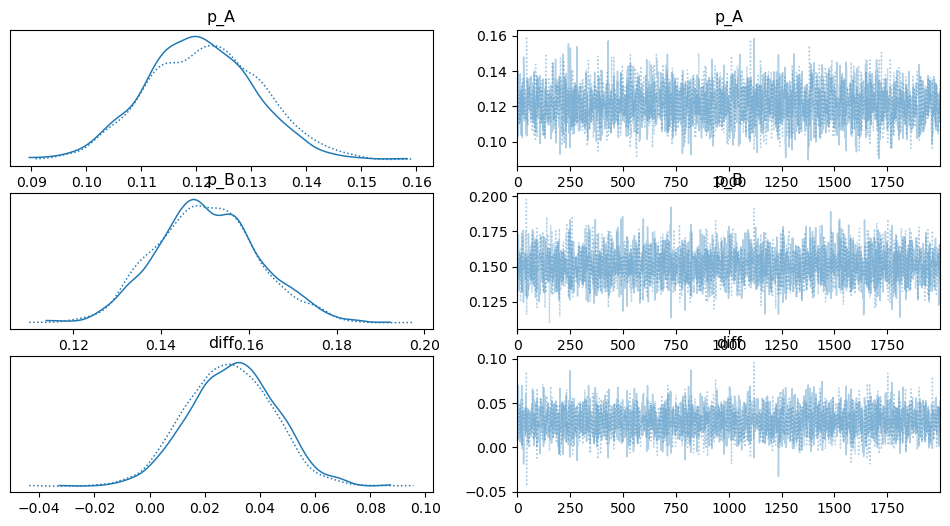
위 코드를 실행하고 결과를 시각화하면, 모델은 오직 ‘새로운 데이터’ 에만 의존하여 결론을 내립니다.

# 결과 시각화
az.plot_trace(trace_uninformative)
plt.show()

# 사후 분포 요약
az.summary(trace_uninformative, var_names=["p_A", "p_B", "diff"], round_to=2)

2. 사전 지식이 있는 경우

이번에는 우리의 마케팅 팀이 과거 유사한 캠페인 데이터에서 전환율이 평균 10% 정도였다는 정보를 가지고 있다고 가정해 봅시다. 이 정보를 모델에 추가하여 다시 한번 모델링 해보겠습니다.

간단하게 이 정보를 사전분포에 반영만 하면 되는 것입니다!

import pymc as pm
import arviz as az
import matplotlib.pyplot as plt

# 데이터는 동일
trials = 1000
conversions_a = 120
conversions_b = 150

with pm.Model() as informative_ab_test:
    # 사전 분포(Prior)에 과거 데이터 기반의 정보 추가
    p_A = pm.Beta("p_A", alpha=10, beta=90)
    p_B = pm.Beta("p_B", alpha=10, beta=90)

    # 우도 함수(Likelihood)는 데이터에 따라
    y_A = pm.Binomial("y_A", n=trials, p=p_A, observed=conversions_a)
    y_B = pm.Binomial("y_B", n=trials, p=p_B, observed=conversions_b)
    
    diff = pm.Deterministic("diff", p_B - p_A)

    # 추론 실행
    trace_informative = pm.sample(2000, tune=1000, cores=1, random_seed=42)

# 결과 시각화 및 요약
az.plot_trace(trace_informative)
plt.show()
az.summary(trace_informative, var_names=["p_A", "p_B", "diff"], round_to=2)

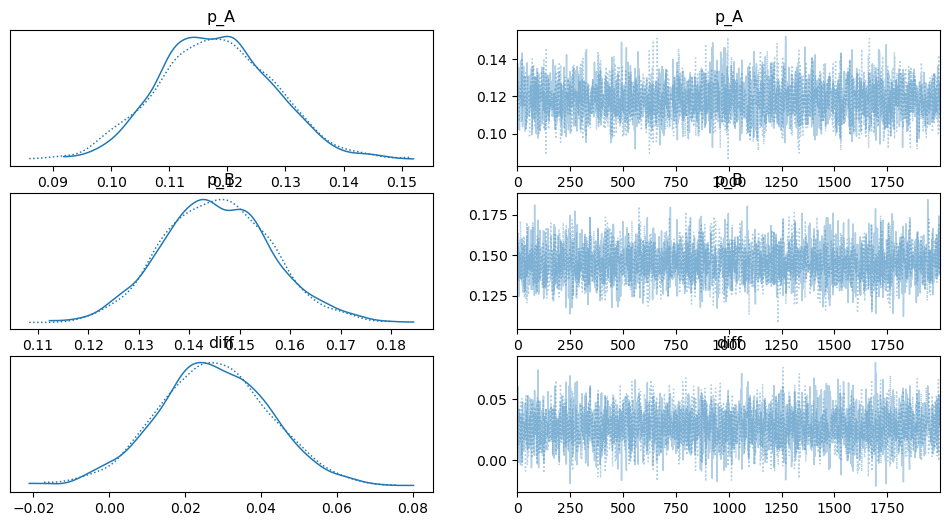
사전정보가 없는 경우와 주어진 경우의 결과를 비교해보겠습니다.

항목	사전 지식 없음	사전 지식 있음	해석
`p_A` 평균	0.12	0.11	데이터(12%)에만 의존한 반면, 사전 지식이 있는 모델은 기존 지식(10%)을 반영해 평균이 약간 낮아짐.
`p_B` 평균	0.15	0.14	마찬가지로, 사전 지식의 영향으로 평균이 기존 데이터(15%)보다 1% 낮게 추론됨.
`diff` 평균	0.03	0.03	두 모델 모두 A와 B의 차이가 3% 근처일 것으로 추론.
`diff` 95% 신뢰구간	`[0.00, 0.06]`	`[-0.00, 0.05]`	핵심 차이: 사전 지식 없는 모델은 차이가 0보다 크다고 결론냈지만, 사전 지식이 있는 모델은 아주 미세하게나마 음수가 될 가능성까지 고려함.

이번에는 방문자 수를 극단적으로 줄여 사전지식의 영향을 확인해보려고 합니다.

방문자수 n이 작은 상황

먼저, 데이터가 매우 적을 때 어떤 결론이 나오는지 확인해봅시다. 기존처럼 아무런 사전 정보 없이 진행합니다.

실험 상황:

A 페이지: 10명 중 1명이 구매
B 페이지: 10명 중 2명이 구매

import pymc as pm
import arviz as az
import matplotlib.pyplot as plt

# 데이터가 매우 적은 경우
trials = 10
conversions_a = 1
conversions_b = 2

with pm.Model() as uninformative_ab_test_small_data:
    p_A = pm.Beta("p_A", alpha=1, beta=1)
    p_B = pm.Beta("p_B", alpha=1, beta=1)
    
    y_A = pm.Binomial("y_A", n=trials, p=p_A, observed=conversions_a)
    y_B = pm.Binomial("y_B", n=trials, p=p_B, observed=conversions_b)
    
    diff = pm.Deterministic("diff", p_B - p_A)

    trace_uninformative_small = pm.sample(2000, tune=1000, cores=1, random_seed=42)
    
az.plot_trace(trace_uninformative_small)
plt.show()
az.summary(trace_uninformative_small, var_names=["p_A", "p_B", "diff"], round_to=2)

이제 데이터는 여전히 적지만, 과거의 경험(사전 지식) 을 가지고 있는 경우를 보겠습니다. 기존에 사용했던 Beta(10, 90) 사전 분포를 그대로 사용합니다.

import pymc as pm
import arviz as az
import matplotlib.pyplot as plt

# 데이터는 그대로 적은 상태
trials = 10
conversions_a = 1
conversions_b = 2

with pm.Model() as informative_ab_test_small_data:
    # 사전 분포(Prior)에 과거 데이터 기반의 정보 추가
    p_A = pm.Beta("p_A", alpha=10, beta=90)
    p_B = pm.Beta("p_B", alpha=10, beta=90)
    
    y_A = pm.Binomial("y_A", n=trials, p=p_A, observed=conversions_a)
    y_B = pm.Binomial("y_B", n=trials, p=p_B, observed=conversions_b)
    
    diff = pm.Deterministic("diff", p_B - p_A)

    trace_informative_small = pm.sample(2000, tune=1000, cores=1, random_seed=42)
    
az.plot_trace(trace_informative_small)
plt.show()
az.summary(trace_informative_small, var_names=["p_A", "p_B", "diff"], round_to=2)

두 그림은 베이지안 모델링에서 사전 지식이 얼마나 중요한 역할을 하는지 보여줍니다. 가장 큰 차이점은 바로 ‘분포의 넓이(불확실성)’ 입니다.

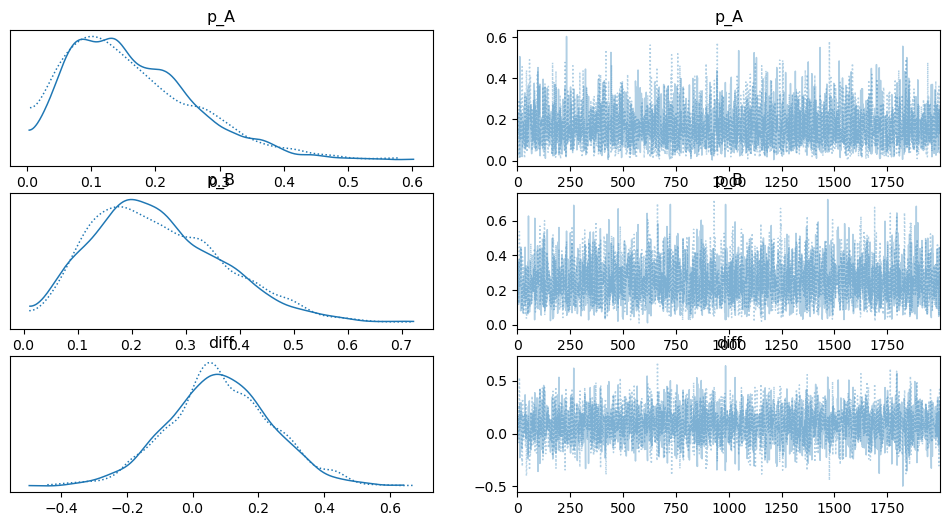
이 그래프는 데이터가 10개밖에 없을 때, 아무런 사전 지식 없이 얻은 결과입니다.

분포의 넓이: p_A, p_B, diff의 분포가 모두 매우 넓게 퍼져 있습니다. 이는 모델이 ‘10개 데이터만으로는 아무것도 확신할 수 없다’고 말하는 것과 같습니다.

diff의 범위: 두 전환율의 차이를 나타내는 diff의 분포가 -0.4부터 0.7까지 넓게 퍼져 있습니다. 이는 A와 B 페이지의 차이가 크지 않거나, 심지어 B가 더 나쁠 수도 있다는 가능성까지 모두 포함하고 있어, 결론을 내리기 매우 어렵습니다.

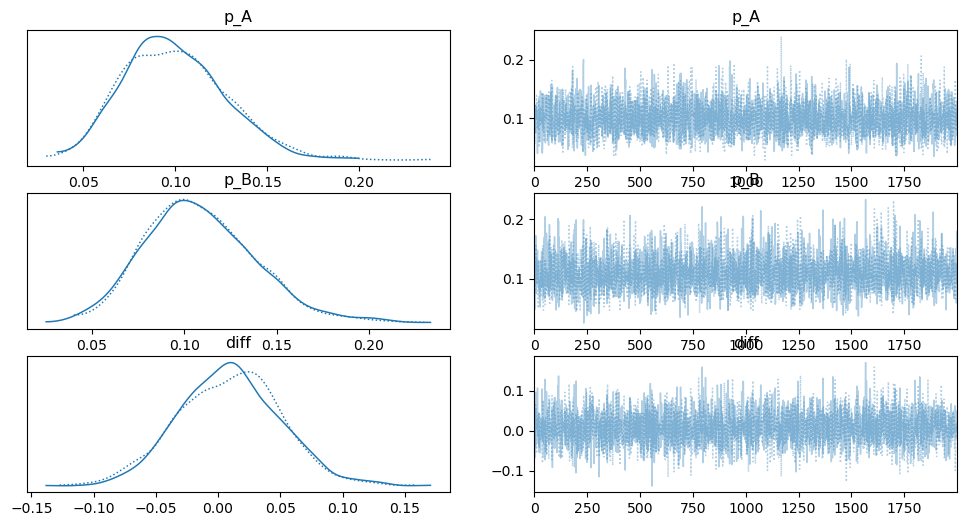
이 그래프는 데이터는 여전히 10개이지만, ‘전환율은 10% 근처일 것이다’라는 사전 지식을 추가했을 때의 결과입니다.

분포의 넓이: 첫 번째 그래프와 비교했을 때, 모든 분포가 훨씬 좁고 봉우리가 높아졌습니다. 이는 사전 지식 덕분에 모델의 불확실성이 크게 줄어들었음을 의미합니다.

diff의 범위: diff의 분포가 좁아져 -0.15부터 0.15 사이로 명확하게 범위가 정해졌습니다. 모델은 ‘A와 B의 차이가 0.03 근처일 가능성이 가장 높고, 94%의 확률로 이 좁은 범위 안에 있다’고 훨씬 더 자신감 있게 말할 수 있게 된 것입니다.

데이터가 적으며 사전정보가 없는 경우와 주어진 경우의 결과를 비교해보겠습니다.

항목	사전 지식 없음	사전 지식 있음	해석
`p_A` 평균	0.16	0.10	데이터(16%)에만 의존한 반면, 사전 지식이 있는 모델은 기존 지식(10%)을 반영해 평균이 약간 낮아짐.
`p_B` 평균	0.25	0.11	마찬가지로, 사전 지식의 영향으로 평균이 기존 데이터(20%)보다 1% 낮게 추론됨.
`diff` 평균	0.08	0.01	사전 지식의 영향을 크게 받아 두 페이지의 차이가 크지 않을 것이라 추론.
`diff` 95% 신뢰구간	`[0.00, 0.06]`	`[-0.00, 0.05]`	핵심 차이: 불확실성이 극적으로 감소하며, 신뢰할 수 있는 결론을 얻게 됨.

결론: 데이터와 지식의 결합

이번 A/B 테스트 예제를 통해 우리는 베이지안 모델링의 핵심적인 특징을 확인할 수 있었습니다.

데이터가 많을 때 (n=1000): 사전 지식이 있든 없든, 추론 결과는 거의 비슷했습니다. 이는 충분한 데이터가 있다면, 데이터 자체가 강력한 증거가 되어 초기 믿음(사전 분포)을 압도한다는 것을 의미합니다.

데이터가 적을 때 (n=10): 사전 지식의 중요성이 극명하게 드러났습니다. 사전 지식이 없으면 모델의 불확실성이 너무 커서 어떤 유의미한 결론도 내릴 수 없었습니다. 하지만 과거의 경험이라는 사전 지식을 추가하자, 모델은 훨씬 안정적이고 신뢰할 수 있는 결론을 내릴 수 있었습니다.

베이지안 추론은 이처럼 우리가 이미 알고 있는 지식(Prior) 을 새롭게 관찰된 데이터(Likelihood) 와 결합하여, 더욱 합리적인 결론(Posterior) 에 도달하게 해주는 강력한 프레임워크입니다. PyMC와 같은 도구 덕분에 우리는 이런 복잡한 추론 과정을 몇 줄의 코드로 간단하게 구현하고, 불확실성을 수치로 표현하며 더 나은 의사결정을 내릴 수 있습니다. 감사합니다.

X Facebook LinkedIn Bluesky

Junhee Kim

PyMC를 이용한 확률적 프로그래밍 입문

Introduction

실험 상황: 두 개의 랜딩 페이지

PyMC 모델링

1. 사전지식이 없는 경우

2. 사전 지식이 있는 경우

방문자수 n이 작은 상황

결론: 데이터와 지식의 결합

공유하기

참고

[Paper Review] Bayesian graph convolutional neural networks for semi-supervised classification

Moran’s I Statistics

[Paper Review] Make Me a BNN: A Simple Strategy for Estimating Bayesian Uncertainty from Pre-trained Model

[Paper Review] Normalizing Flows: Probabilistic Modeling and Inference