Bayesian Online Change Point Detection
이 포스팅은 Bayesian Online Changepoint Detection에 대한 글입니다.
Introduction
변화점 탐지란?
변화점 탐지(Changepoinrt Detection)은 시계열 데이터에서 통계적 성질이 변화하는 지점을 찾아내는 문제입니다. 예를 들어, 평균이나 분산이 급격하게 변화하거나, 데이터의 생성 프로세스가 달라지는 순간을 “변화점” 이라고 합니다.

이 데이터에서는 평균이 급격하게 변화하는 모습을 볼 수 있네요
변화점 탐지는 크게 두 가지로 나누어 볼 수 있습니다.
1. Offline Changepoint Detection
- 전체 데이터가 확보되었을 떄, 사후적으로 변화점을 찾는 방식
- 참고 : C.Truong, Selective review of offline change point detection methods
2. Online Changepoint Detection
-
데이터가 순차적으로 들어오는 상황에서 새로운 관측치가 들어오자마자 실시간으로 변화점을 추정하는 방식
Why Bayesian?
온라인 변화점 탐지(Online CPD)의 핵심은 새로운 데이터가 들어올 때마다 “지금 변화가 일어났는가?”를 판단하는 것입니다.
즉, 관측치가 한 점씩 순차적으로 추가될 때, 우리는 매번 변화점인지의 여부를 추론해야 합니다.
이 상황에서 Bayesian 접근이 특히 잘 맞는 이유는 다음과 같습니다:
\[P(\theta \mid x_{1:t}) \propto P(x_t \mid \theta) \cdot P(\theta \mid x_{1:t-1})\]즉, 새로운 데이터 $x_t$가 들어올 때마다 이전 시점의 사후분포 $P(\theta \mid x_{1:t-1})$는
그 자체로 다음 단계의 사전분포(prior)가 되어, 매 시점마다 자연스럽게 갱신됩니다.
이처럼 사후분포를 곧바로 다음 단계의 사전분포로 이어 붙이는 구조가 바로
Bayesian 추론의 핵심 메커니즘이며, 실시간으로 변화 가능성을 갱신해야 하는 온라인 변화점 탐지 문제와
아주 잘 들어맞습니다.
Main Idea of BOCD
Bayesian Online Changepoint Detection (Adams & MacKay, 2007)는 위와 같은 베이지안 프레임워크를 온라인 변화점 탐지 문제에 적용한 대표적인 방법입니다.
Run Length
핵심은 Run-Length 라는 개념입니다.
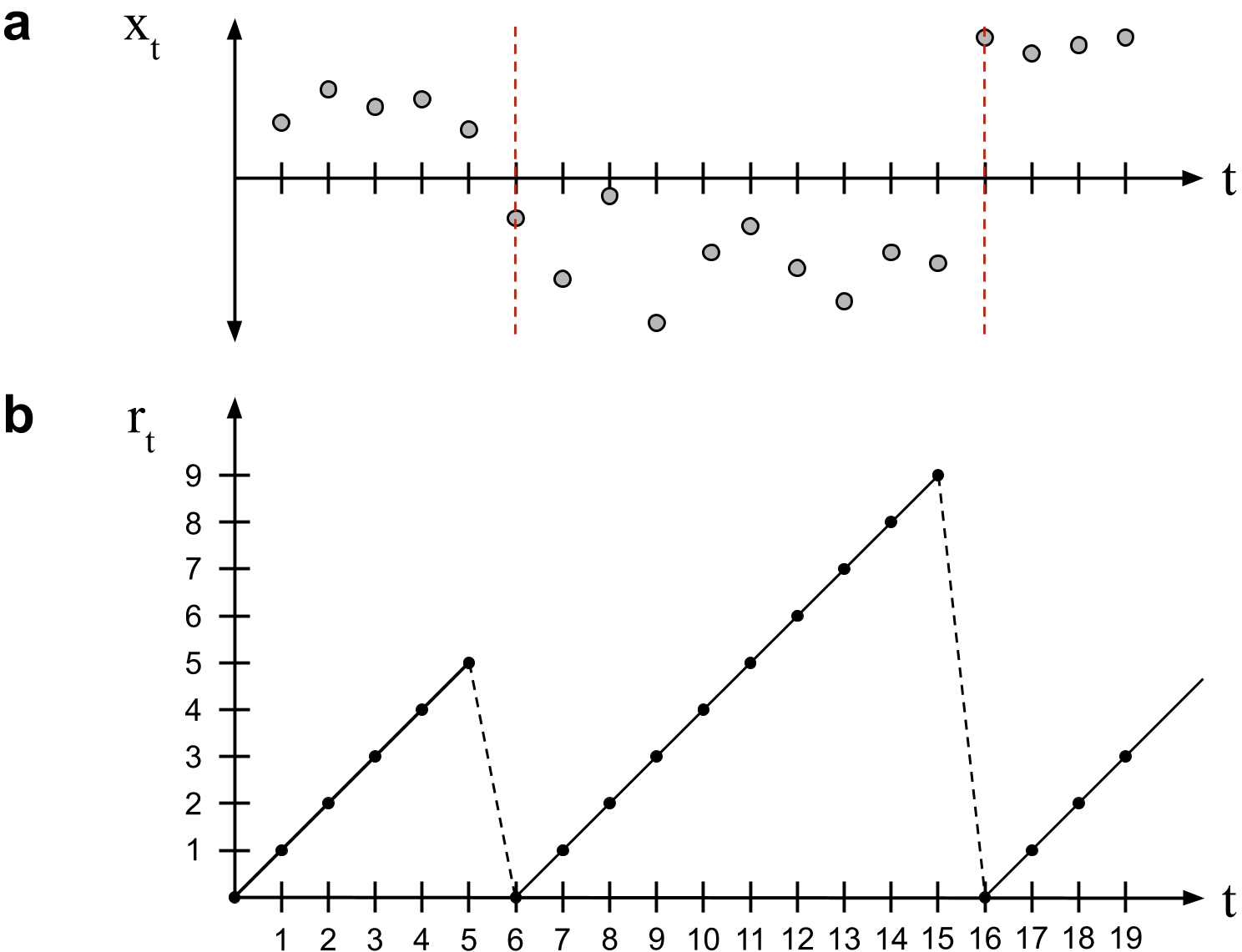
위 그림에서 $b$축이 Run Length를 의미합니다. 2개의 빨간 점선이 변화점인 상황에서 2회 증가하다 감소하는 것을 볼 수 있습니다.
정리하면 다음과 같습니다.
-
$r_t$ : 현재 시점 $t$에서 마지막 변화점 이후의 데이터의 길이
- 만약 변화점이 방금 일어났다면 $r_t = 0 $
- 변화점이 없고 동일한 생성 프로세스가 이어진다면, $r_t$는 계속 증가
이제 BOCD는 매 시점마다 Run Length의 분포 $P(r_t \mid x_{1:t})$를 추정하여, 새로운 데이터가 들어올 때 변화점일 확률을 계산하게 됩니다.
Hazard Function (위험 함수)
변화가 발생할 확률은 Hazard Function $H(r)$ 으로 정의됩니다.
이는 “run length가 $r$일 때, 다음 시점에 변화점이 발생할 확률”을 나타냅니다:
반대로 변화점이 발생하지 않고 run length가 하나 증가할 확률은:
\[P(r_t = r+1 \mid r_{t-1} = r) = 1 - H(r)\]예시: 기하분포 기반 Hazard Function
가장 단순하게 위험함수를 설정하는 것은 평균 구간 길이가 $\lambda$라고 가정하는 것입니다.
이때 Hazard Function은 상수로:
- $\lambda = 100$ 이라면, 평균적으로 100 포인트마다 변화가 일어난다고 보는 것
- 따라서 어떤 시점이든 약 1% 확률로 변화가 발생한다고 가정하는 셈입니다.
Posterior Recursion (사후분포 재귀식)
BOCPD는 각 시점 $t$에서 run length 분포 $P(r_t \mid x_{1:t})$를 유지합니다.
새로운 데이터 $x_t$가 들어올 때마다, 다음 두 가지 경우로 나눠서 확률을 갱신합니다.
1. 변화점이 발생한 경우 (run length = 0)
마지막 변화점이 방금 발생했다면, \(P(r_t = 0, x_{1:t}) = \sum_{r_{t-1}} P(r_{t-1}, x_{1:t-1}) \cdot H(r_{t-1}) \cdot P(x_t \mid \text{new segment})\)
여기서 $H(r_{t-1})$는 run length가 $r_{t-1}$일 때 변화점이 발생할 확률입니다.
2. 변화점이 발생하지 않은 경우 (run length 증가)
변화점이 발생하지 않았다면 run length가 하나 늘어나게 됩니다: \(P(r_t = r_{t-1}+1, x_{1:t}) = P(r_{t-1}, x_{1:t-1}) \cdot (1 - H(r_{t-1})) \cdot P(x_t \mid r_{t-1})\)
즉, 직전 run length에서 “변화 없음”이 선택된 경우의 확률을 그대로 이어받아 업데이트합니다.
3. 정규화 (Normalization)
위 두 경우를 모두 계산한 뒤, 전체 확률이 1이 되도록 정규화합니다:
\[P(r_t \mid x_{1:t}) = \frac{P(r_t, x_{1:t})}{\sum_{r_t} P(r_t, x_{1:t})}\]이 재귀식 덕분에 BOCPD는 매 시점마다 변화점 확률과 run length 분포를 효율적으로 갱신할 수 있습니다.
즉, 데이터를 처음부터 끝까지 다시 계산하지 않고, 이전 단계 결과만으로 빠르게 업데이트가 가능합니다.
Exmaple: Gaussian-Gaussian Model
BOCPD에서 관측 데이터 $x_t$가 정규분포로부터 생성된다고 가정해보겠습니다.
\[x_t \sim \mathcal{N}(\mu, \sigma^2), \quad \sigma^2 \text{는 알려져 있음}\]여기서 변화점이 발생하면 평균 $\mu$가 새로운 값으로 리셋된다고 가정합니다.
사전분포 (Prior)
평균 $\mu$에 대해 정규분포를 사전분포로 둡니다:
\[\mu \sim \mathcal{N}(\mu_0, \tau_0^2)\]사후분포 (Posterior)
새로운 데이터 $x_t$가 들어오면,
사후분포 역시 정규분포 형태(Conjugate prior)로 유지될 수 있습니다:
업데이트 규칙은 알려진 Conjugate Normal형태에 의해 다음과 같습니다:
\[\tau_t^2 = \left( \frac{1}{\tau_{t-1}^2} + \frac{1}{\sigma^2} \right)^{-1}, \quad \mu_t = \tau_t^2 \left( \frac{\mu_{t-1}}{\tau_{t-1}^2} + \frac{x_t}{\sigma^2} \right)\]즉, 새로운 데이터가 들어올 때마다 평균에 대한 불확실성을 줄여가며 업데이트합니다.
예측 분포 (Predictive Distribution)
BOCPD는 다음 데이터 $x_{t+1}$이 나올 확률도 필요합니다.
이는 Student-t 분포로 계산되며, 재귀 업데이트 과정에서 사용됩니다:
이 Gaussian-Gaussian 예시는 BOCPD의 작동 원리를 보여주는 가장 기본적인 케이스입니다.
실제 구현에서는 이 예측분포를 사용해 변화점 발생 확률을 계산하고,
앞서 설명한 Posterior Recursion에 대입하여 run length 분포를 갱신하게 됩니다.
Code
아래 코드는 Gaussian-Gaussian 모델을 기반으로 한 BOCPD의 핵심 아이디어를 구현한 간단 예시입니다.
import numpy as np
from scipy.stats import norm
# --------------------------
# Hazard function (상수형)
# --------------------------
def constant_hazard(lam, r):
return 1.0 / lam * np.ones(r.shape)
# --------------------------
# BOCPD 실행
# --------------------------
def bocpd(data, hazard_func, lam=100, mu0=0, tau0=1, sigma=1):
T = len(data)
R = np.zeros((T+1, T+1)) # run length posterior
R[0,0] = 1
# 사전분포 파라미터
mu_t = np.array([mu0])
tau_t2 = np.array([tau0**2])
for t in range(1, T+1):
x = data[t-1]
# 예측 분포
pred_prob = norm.pdf(x, mu_t, np.sqrt(sigma**2 + tau_t2))
# 성장 단계 (run length 증가)
growth_probs = R[t-1, :t] * (1 - hazard_func(lam, np.arange(t))) * pred_prob
R[t,1:t+1] = growth_probs
# 변화 단계 (run length = 0)
cp_prob = np.sum(R[t-1, :t] * hazard_func(lam, np.arange(t)) * pred_prob)
R[t,0] = cp_prob
# 정규화
R[t,:t+1] /= np.sum(R[t,:t+1])
# 파라미터 업데이트 (conjugate Gaussian)
tau_t2 = 1.0 / (1.0/tau_t2 + 1.0/sigma**2)
mu_t = tau_t2 * (mu_t/tau_t2 + x/sigma**2)
return R
# --------------------------
# 실행 예시
# --------------------------
np.random.seed(42)
data = np.concatenate([
np.random.normal(0, 1, 50),
np.random.normal(5, 1, 50)
])
R = bocpd(data, constant_hazard, lam=50)
import matplotlib.pyplot as plt
plt.imshow(np.log(R+1e-6).T, aspect='auto', origin='lower')
plt.colorbar(label="log P(run length)")
plt.xlabel("time")
plt.ylabel("run length")
plt.title("BOCPD run length posterior")
plt.show()
위 결과 그림에서, run length posterior가 특정 지점에서 갑자기 0으로 리셋되는 패턴이 보이면, 그 지점이 곧 변화점(changepoint) 으로 탐지된 것으로 볼 수 있습니다.
잘 알려진 R 패키지 ocp를 통해 데이터에 쉽게 적용도 가능합니다.
References
-
Adams, R. P., & MacKay, D. J. C. (2007). Bayesian Online Changepoint Detection.
-
Fearnhead, P., & Liu, Z. (2007). On-line Inference for Multiple Changepoint Problems.

댓글남기기