[Paper Review] Compact Memory for K-prior Based Continual Learning
이 포스팅은 지속학습(Continual Learning)에서의 K-prior 기반 Compact Memory 논문 “Compact Memory for K-prior Based Continual Learning”을 정리한 글입니다.
TL;DR
- 문제의식: 단순 Regularization(Elastic Weight Consolidation, L2 Penalty, Knowledge Distilation 등)는 과거 전체 데이터를 본 배치 SGD에 비해 그래디언트를 재현하지 못하여 성능 격차가 발생합니다.
- 핵심 아이디어: 데이터 원본 대신 특징공간의 기저 벡터(basis) 를 저장하여 작은 메모리로도 과거 그래디언트를 복원합니다.
- 선형 회귀: Hessian Matching으로 과거+현재 특징 구조를 정확히 보존합니다.
- 로지스틱 회귀: 가중 Hessian을 반영한 PPCA-EM 근사를 제안합니다.
- 실험: Split-MNIST, Two-Moon에서 작은 메모리로도 배치 학습에 가까운 성능을 달성합니다.
Introduction: Lack of Regularization methods
- EWC, L2, 지식증류 같은 정규화는 “이전 파라미터 근처에 머물라” 는 제약일 뿐입니다.
즉, 과거 전체 데이터가 만들어내던 정확한 그래디언트 방향을 복원하지 못합니다. - 따라서 배치 학습(Batch Learning) 대비 성능이 뒤쳐집니다.
- 이를 해결하기 위해서는, 과거 데이터가 만들어내던 그래디언트 자체를 재구성해야 합니다.
K-prior & Gradient Reconstruction
- K-prior의 목표는 현재 정규항의 그래디언트가 과거 모든 태스크의 평균 손실 그래디언트 합과 같아지도록 설계하는 것입니다.
- 즉, 배치 학습과 동일한 업데이트 방향을 만드는 것입니다.
- 그러나 실제로는 보통 Replay Method를 사용하기 때문에 메모리 부담이 큽니다.
- 본 논문은 이를 Feature Space의 Basis를 저장하는 방식으로 구현합니다.
Compact Memory
- 원본 데이터 대신, 특징공간의 공분산/Hessian 구조를 소수의 기저 벡터 $U_t = [u_1, \dots, u_K]$로 압축 저장합니다.
- 이렇게 하면 메모리 사용량은 데이터 수가 아니라 랭크(rank) 에만 비례합니다.
- 이 기저만 있으면 과거 그래디언트를 복원할 수 있습니다.
Linear Regression: Hessian Matching
핵심 수식
\(U_{t+1} U_{t+1}^\top \;=\; \Phi_{t+1}\Phi_{t+1}^\top \;+\; U_t U_t^\top\)
- $\Phi_{t+1}$: 새 태스크 특징행렬
- 의미: 과거+현재 공분산 구조를 보존하는 새로운 기저 $U_{t+1}$을 찾는 것입니다.
구현 A: SVD
- 단순한 방법은 $[U_t, \Phi_{t+1}]$에 대해 SVD를 수행하여 상위 $K$ 좌특이벡터를 취하는 것입니다.
구현 B: PPCA-EM
- 확률적 PCA(Probabilistic PCA)의 EM 알고리즘을 사용합니다.
- E-step: 잠재 변수 $Z$를 추정합니다.
- M-step: $U_{t+1}$을 갱신합니다.
- 결과적으로 과거+현재 특징을 모두 잘 설명하는 기저가 자동으로 추출됩니다.
Logistic Regression: Weighted Hessian & PPCA-EM
로지스틱은 비선형이므로 단순 $X^\top X$가 아니라 가중치 포함 Hessian이 필요합니다.
수식
\(U_{t+1} W_{t+1} U_{t+1}^\top \;=\; \Phi_{t+1} B_{t+1} \Phi_{t+1}^\top \;+\; U_t W_t U_t^\top\)
- $B_{t+1}$: 새로운 데이터의 가중치 대각행렬
- $W_t$: 과거 기저의 가중치
- 가중치 추정은 $\tilde u_{k} = \sqrt{w_k} u_k$ 형태로 변환하여 PPCA-EM으로 근사합니다.
Algorithm 1 (Appendix A.1)
- K-prior로 $\theta_{t+1}$을 학습합니다.
- 블록 행렬 $[\,\Phi_{t+1}B_{t+1}^{1/2}; U_tW_t^{1/2}\,]$을 구성합니다.
- PPCA-EM으로 $\tilde U_{t+1}$을 추정합니다.
- 벡터 노름을 분리하여 $U_{t+1}, W_{t+1}$을 복원합니다.
→ 선형 회귀는 정확히 재구성할 수 있으며, 로지스틱 회귀는 근사적(거의 최적) 재구성을 달성합니다.
Experiment
Split-MNIST (선형 회귀)
- MNIST를 (0,1), (2,3), …, (8,9) 5개 태스크로 분할합니다.
- 다중 출력 회귀 포맷으로 변환합니다.
- 결과: 작은 메모리에서도 EM이 SVD보다 성능이 우수합니다.
- Fig.2에서는 Hessian의 상위 고유벡터(“eigen-images”)가 시각화됩니다.
Two-Moon (로지스틱 회귀)
- 입력을 다항 특징(7차원)으로 확장합니다.
- 태스크 3개를 순차 학습하며, 메모리를 누적합니다 (7→14→21).
- 결과: 순차 학습 후 결정경계가 배치 학습의 경계에 근접합니다.
Figure 1
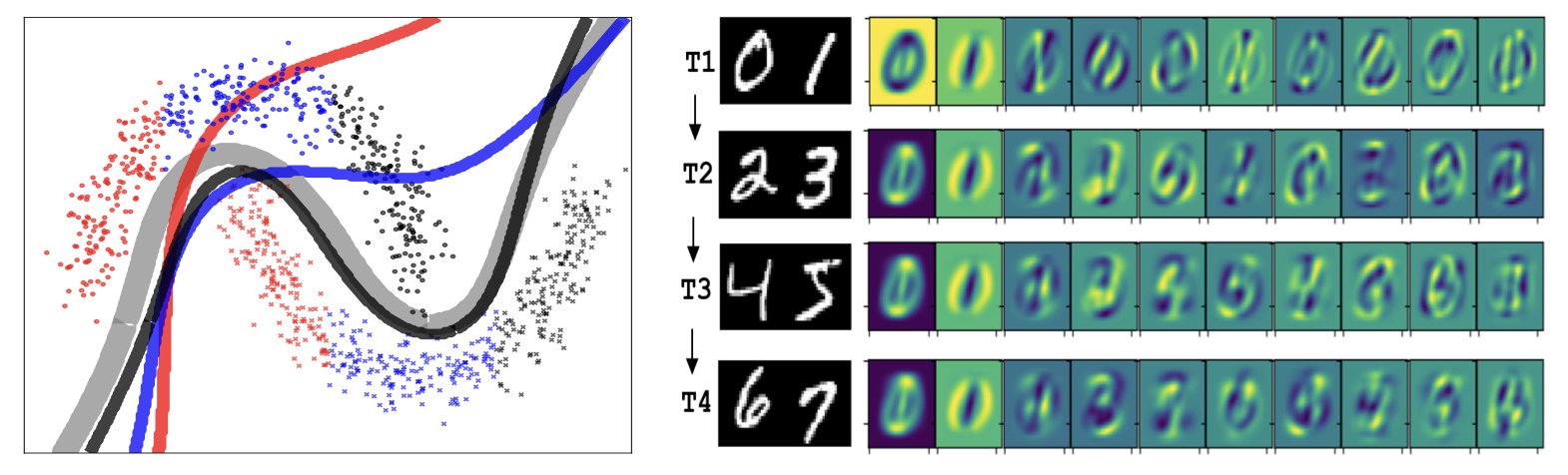
*출처 Compact Memory for K-prior Based Continual Learning
왼쪽 그림 (Two-Moon Classification)
- 데이터: 세 개의 태스크(빨강, 파랑, 검정)를 포함합니다.
- 회색 선: 배치 학습 결과 (ground truth 결정경계)입니다.
- 색깔 선: Compact Memory 기반 순차 학습 결과입니다.
- 결과: 각 태스크당 단 7개 메모리만 사용해도 결정경계가 배치 학습과 거의 일치합니다.
해석: 아주 작은 메모리로도 배치 학습과 유사한 일반화 성능을 복원할 수 있습니다.
오른쪽 그림 (Split-MNIST Eigen-Images)
- 각 행(Row): 새로운 태스크 추가 시점 (T1: 0vs1, T2: 2vs3, …)입니다.
- 각 열(Column): 고유값 크기 순으로 정렬된 eigen-images입니다.
- 첫 2~3개 eigen-images: 데이터의 핵심 구조를 잘 반영합니다 (숫자 모양이 선명).
- 그 이후 eigen-images: 고유값이 작아지면서 잡음 같은 패턴으로 변합니다 → 덜 중요한 방향입니다.
해석: Compact Memory는 실제 데이터 대신 공분산/Hessian 공간의 “핵심 축”을 저장하고 있음을 시각적으로 보여줍니다.
Contribution
- 단순 정규화는 배치 성능의 한계를 넘지 못합니다. → 본 논문은 그래디언트 재구성 관점을 제시합니다.
- 데이터 부분집합 리플레이 대신, 특징 기저 압축 메모리를 제안합니다.
- 선형 회귀에서는 정확한 Hessian Matching, 로지스틱 회귀에서는 PPCA-EM 근사를 구현합니다.
Application Process
- 특징화: 입력 $\phi(x)$를 준비합니다.
- K-prior 학습으로 $\theta_{t+1}$을 업데이트합니다.
- 메모리 업데이트:
- 선형 회귀: SVD 또는 PPCA-EM으로 Hessian Matching을 수행합니다.
- 로지스틱 회귀: 가중 Hessian을 PPCA-EM으로 근사합니다.
- 메모리 크기 조절: 유효 랭크 수준으로 유지합니다.
Limitation and Future work
- 현재는 작은 데이터/모델에서만 검증되었습니다.
- CNN/Transformer 같은 대규모 모델로의 확장이 필요합니다.
- 로지스틱 회귀에서 이론적 최적 가중치 $w_k^*$는 실제 추정이 어렵기 때문에 근사 방식을 사용합니다.
- 특징 맵 설계, 메모리 크기 스케줄, 하이퍼파라미터 감도에 대한 추가 연구가 필요합니다.
Conclusion
- 정규화는 단순한 안전벨트일 뿐, 배치 그래디언트 방향을 재현하지 못합니다.
- Compact Memory는 데이터 대신 공분산/Hessian 기저를 저장합니다.
- 선형 회귀에서는 정확 재구성이 가능하고,
- 로지스틱 회귀에서는 가중 Hessian을 근사합니다.
- EM은 작은 메모리에서 SVD보다 효과적입니다.

댓글남기기