Variety of Methods for Dimensionality Reduction

이 포스팅은 여러가지 차원축소(Dimensionality Reduction)기법들에 대해 소개하고 간단한 시각화를 해보는 글입니다.

Introduction

차원 축소는 고차원 데이터를 저차원으로 표현하여 시각화,
노이즈 제거, 계산 효율화 등을 가능하게 하는 아주 중요한 기법입니다.

우리는 다음과 같은 흐름으로 기법들을 살펴보려고 합니다.

1. 선형 기법: PCA
2. 확률적/베이지안 확장: PPCA, GPLVM
3. 지도 차원 축소: LDA
4. 비선형 확장: Kernel PCA
5. 매니폴드 학습: LLE, Isomap
6. 최신 시각화 기법: t-SNE, UMAP

---

Dataset & Experimental Setup

모든 그림은 sklearn.datasets.load_digits 데이터셋 으로 생성했습니다.

• 샘플 수 N = 1797, 클래스 수 C = 10 (0–9)
• 원본 특징 차원 D = 64 (8×8 회색조 이미지 벡터화)
• StandardScaler로 표준화
• 비지도 기법은 학습에 레이블 미사용, 단 색상은 레이블로 표시
• 지도 기법(LDA)만 학습에 레이블 사용

plot 하기 위한 함수와 라이브러리를 로드해줍니다.

import os
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_digits
from sklearn.decomposition import PCA, KernelPCA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
from sklearn.manifold import Isomap, LocallyLinearEmbedding, TSNE
from sklearn.preprocessing import StandardScaler
import umap

def plot_embedding(X_embedded, y, title, filename):
    plt.figure(figsize=(6, 5))
    scatter = plt.scatter(X_embedded[:, 0], X_embedded[:, 1], c=y, cmap="tab10", s=10, alpha=0.7)
    plt.colorbar(scatter, ticks=range(10))
    plt.title(title)
    plt.tight_layout()
    plt.savefig(f"assets/img/{filename}", dpi=300)
    plt.close()

---

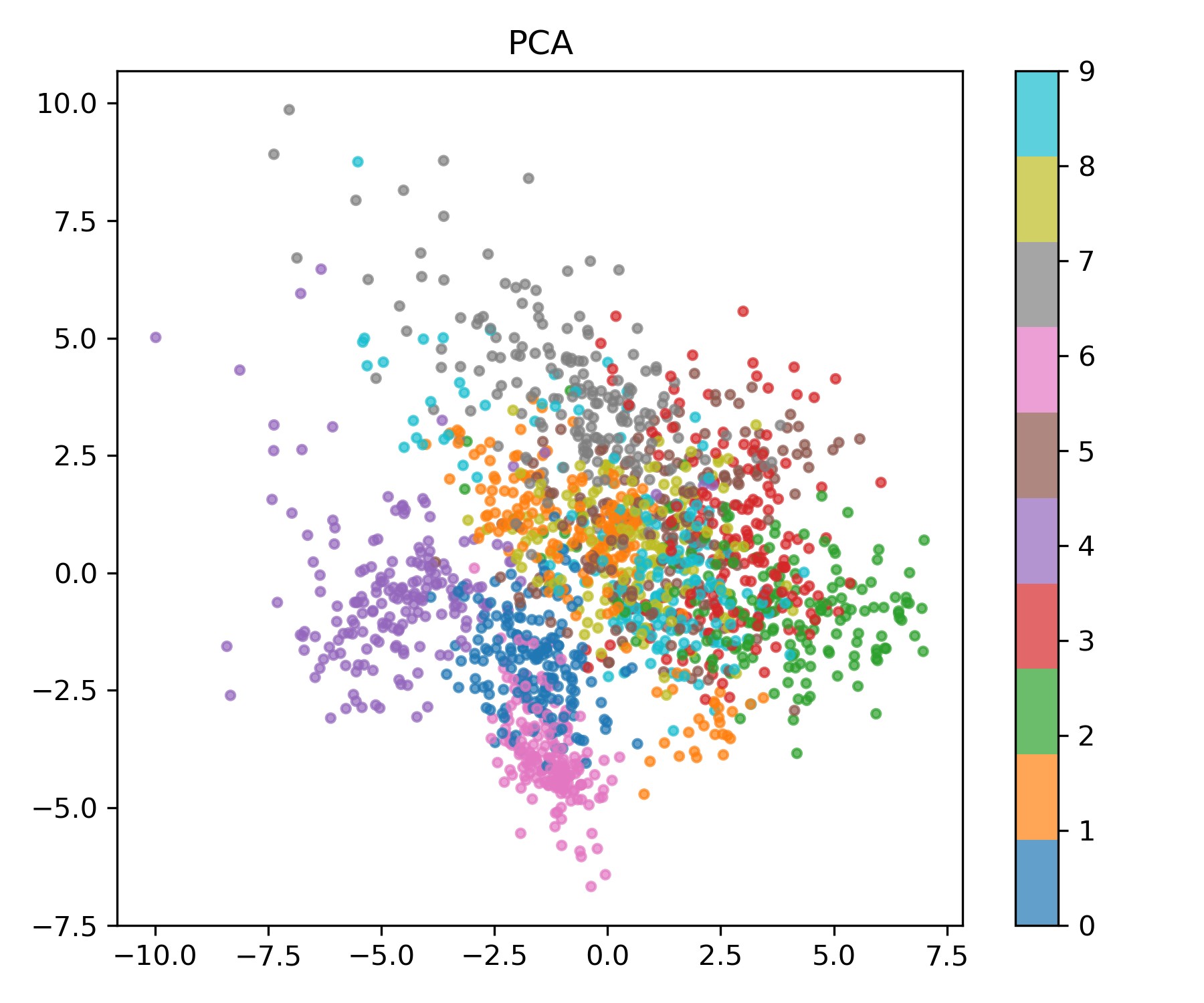
PCA (Principal Component Analysis)

모든 차원 축소 기법의 출발점은 PCA입니다.
데이터의 분산을 가장 크게 설명하는 직교 방향을 찾아 투영합니다.

\[S = \frac{1}{N}\tilde X^\top \tilde X, \quad \tilde X = X - \mathbf{1}\mu^\top\]

고유분해 $S = V\Lambda V^\top$ 를 통해 상위 $k$개 벡터 $V_k$를 선택하고, 투영은 $Z = \tilde X V_k$.

pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)
plot_embedding(X_pca, y, "PCA", "pca_example.png")

PCA Tutorial

---

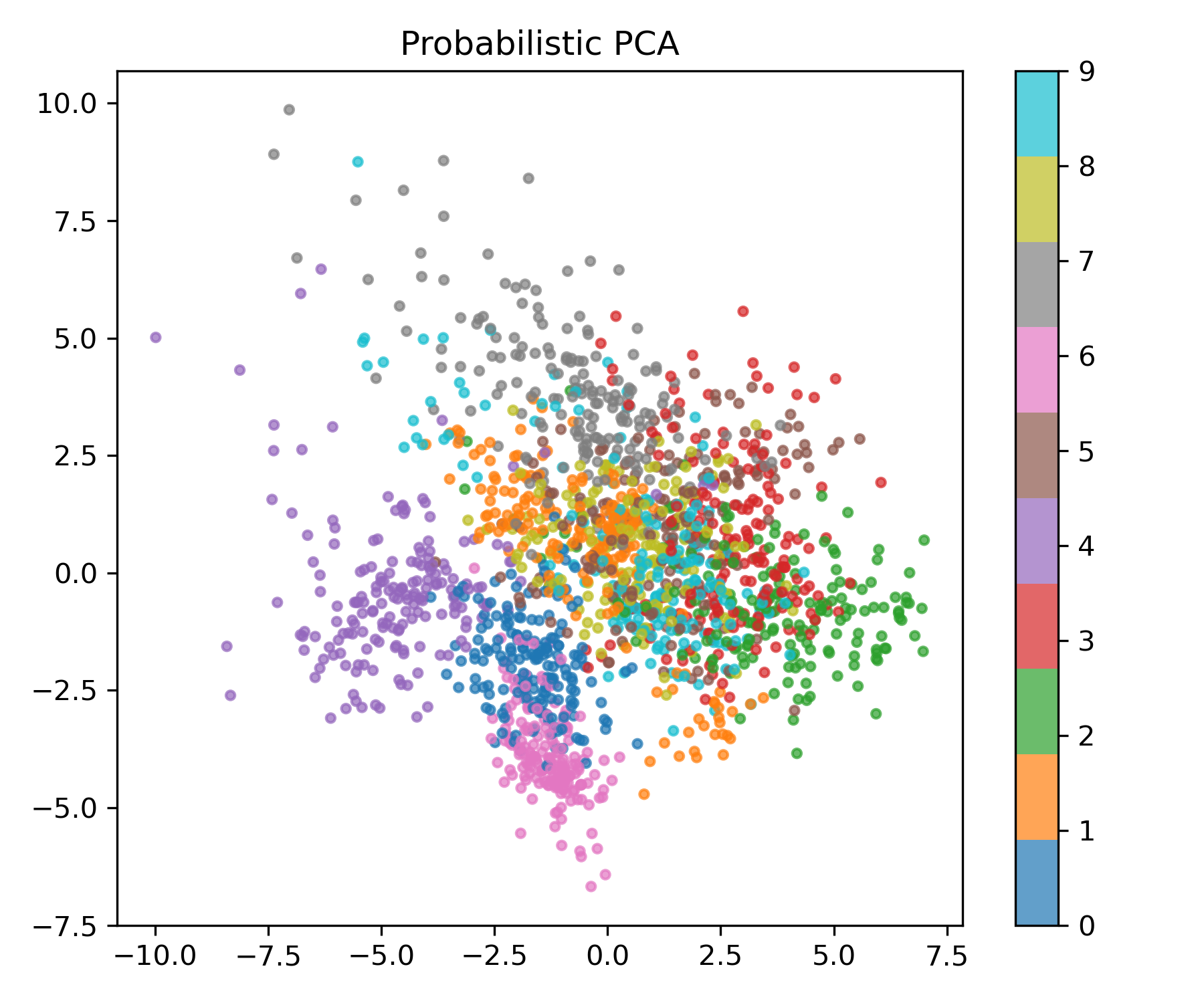
Probabilistic PCA (PPCA)

PCA를 확률적 생성 모델로 해석할 수 있습니다.

\[x = Wz + \mu + \epsilon,\quad z\sim\mathcal N(0,I),\ \epsilon\sim\mathcal N(0,\sigma^2 I)\]

이는 PCA를 베이지안 방법으로 확장할 기반을 마련합니다.

ppca = PCA(n_components=2, svd_solver="full")
X_ppca = ppca.fit_transform(X)
plot_embedding(X_ppca, y, "Probabilistic PCA", "ppca.png")

Tipping & Bishop, 1999

---

GPLVM (Gaussian Process Latent Variable Model)

PPCA는 선형 구조를 가정하지만, GPLVM은 잠재변수 $Z$와 관측 데이터 $Y$ 사이의 관계를 가우시안 프로세스(GP) 로 모델링합니다.

\[Y \sim \mathcal{GP}(0, K(Z,Z))\]

이는 불확실성 추론까지 가능하게 하여, 단순 차원 축소를 넘어 베이지안 representation learning의 출발점이 됩니다.

latent_dim = 2
kernel = GPy.kern.RBF(input_dim=latent_dim, ARD=True)

m = GPy.models.GPLVM(X, input_dim=latent_dim, kernel=kernel)
m.optimize(messages=True, max_iters=200)

Z = m.X.mean.values


plt.figure(figsize=(6, 5))
scatter = plt.scatter(Z[:, 0], Z[:, 1], c=y, cmap="tab10", s=10, alpha=0.7)
plt.colorbar(scatter, ticks=range(10))
plt.title("GPLVM (GPy)")
plt.tight_layout()
plt.savefig("assets/img/gplvm.png", dpi=300)

Lawrence, 2004

---

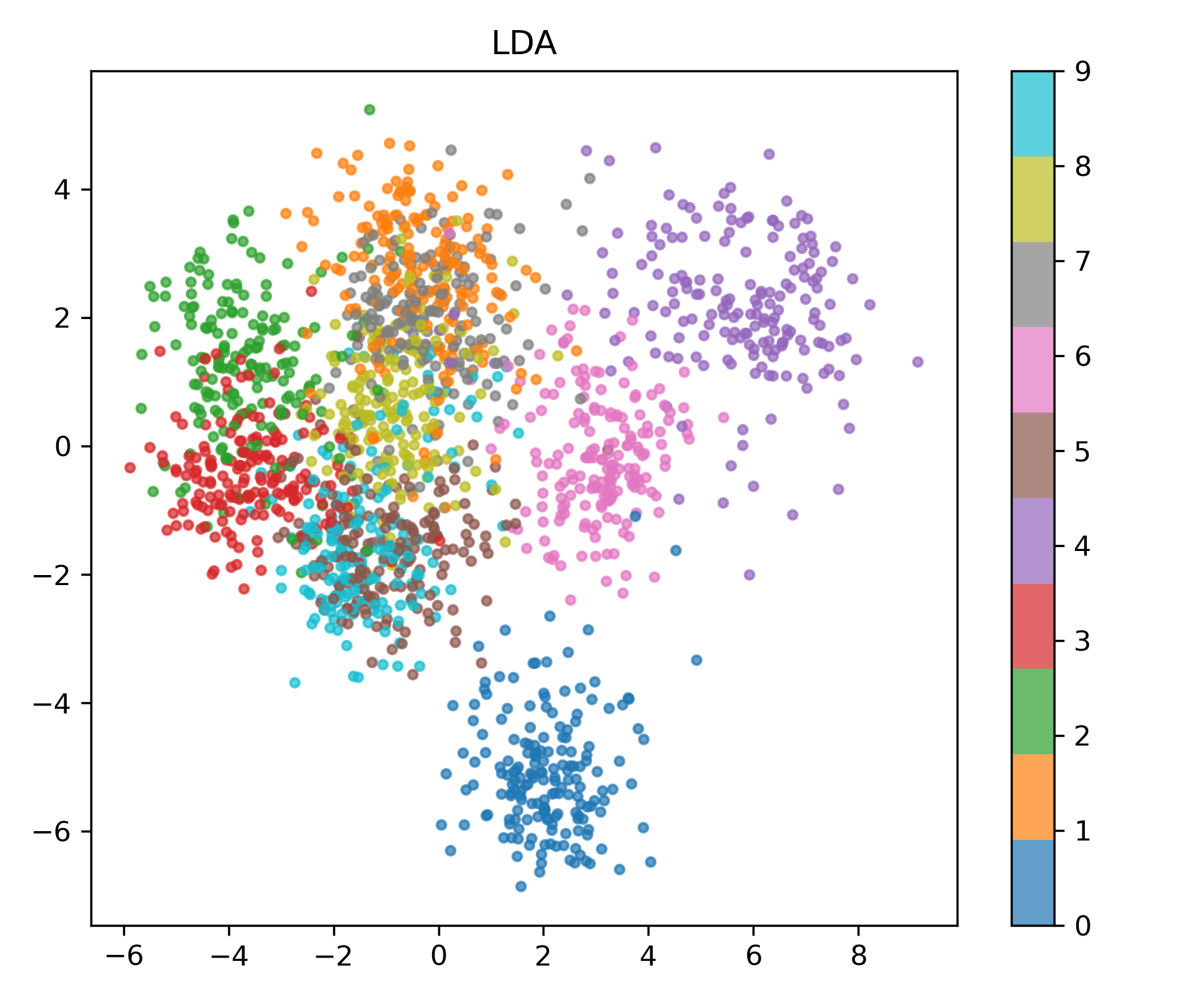
LDA (Linear Discriminant Analysis)

앞선 PCA 계열은 모두 비지도 학습 기법입니다.
하지만 분류(classification) 문제에서는 레이블 정보를 적극적으로 활용하는 것이 더 효과적일 수 있습니다.

LDA는 클래스 간 분산($S_B$)을 극대화하고 클래스 내 분산($S_W$)을 최소화하는 투영을 찾습니다.

\[W^* = \arg\max_W \frac{|W^T S_B W|}{|W^T S_W W|}\]

lda = LDA(n_components=2)
X_lda = lda.fit_transform(X, y)
plot_embedding(X_lda, y, "LDA", "lda.png")

---

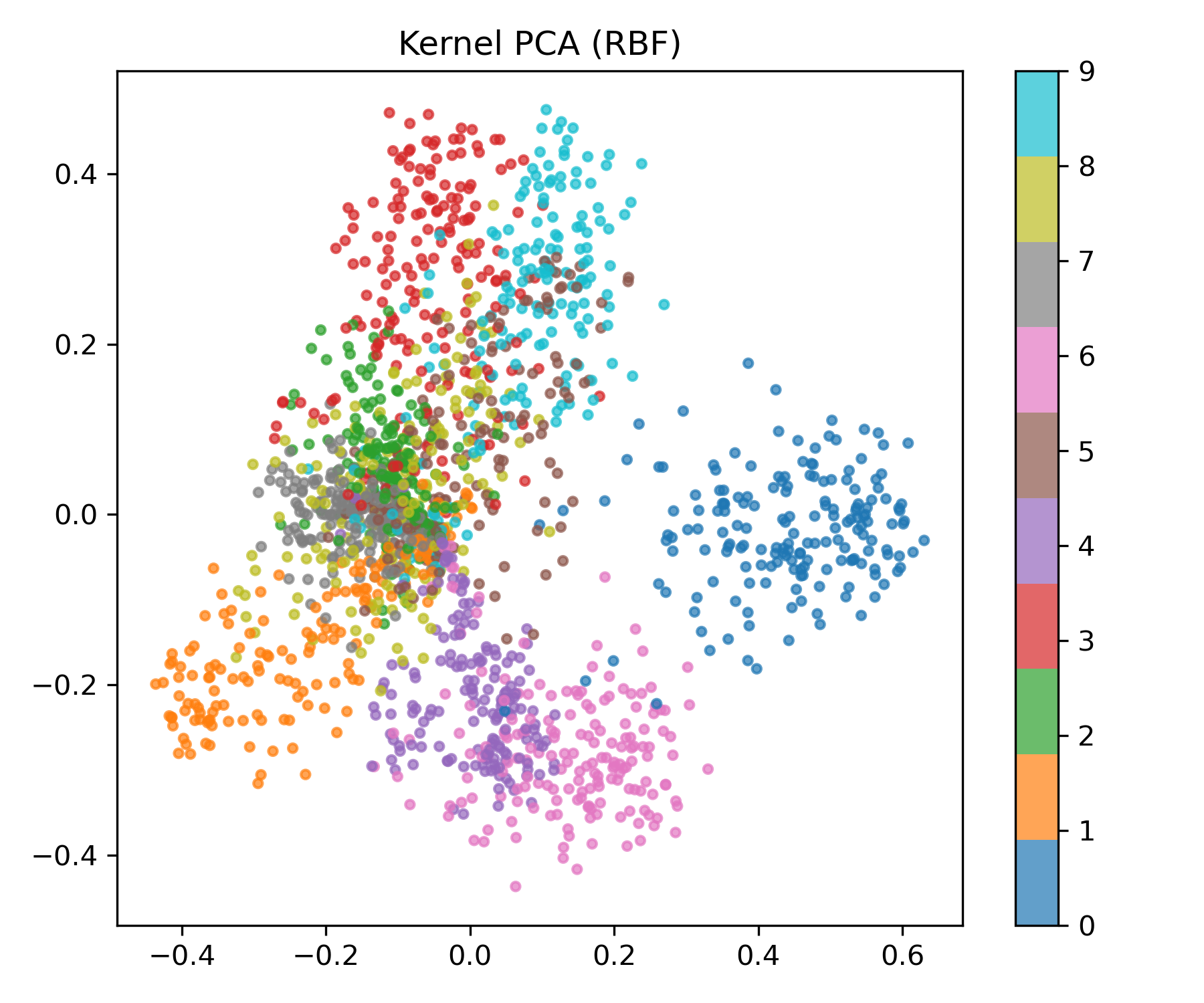
Kernel PCA

이제 선형 방법을 넘어 비선형 구조를 학습해야 할 때가 옵니다.
Kernel PCA는 커널 트릭을 이용해 입력을 고차원 feature space로 사상한 뒤 PCA를 수행합니다.

\[K_{ij} = k(x_i, x_j) = \exp(-\gamma \lVert x_i - x_j \rVert^2)\]

kpca = KernelPCA(n_components=2, kernel="rbf", gamma=0.03)
X_kpca = kpca.fit_transform(X)
plot_embedding(X_kpca, y, "Kernel PCA (RBF)", "kernel_pca.png")

Schölkopf et al., 1998

---

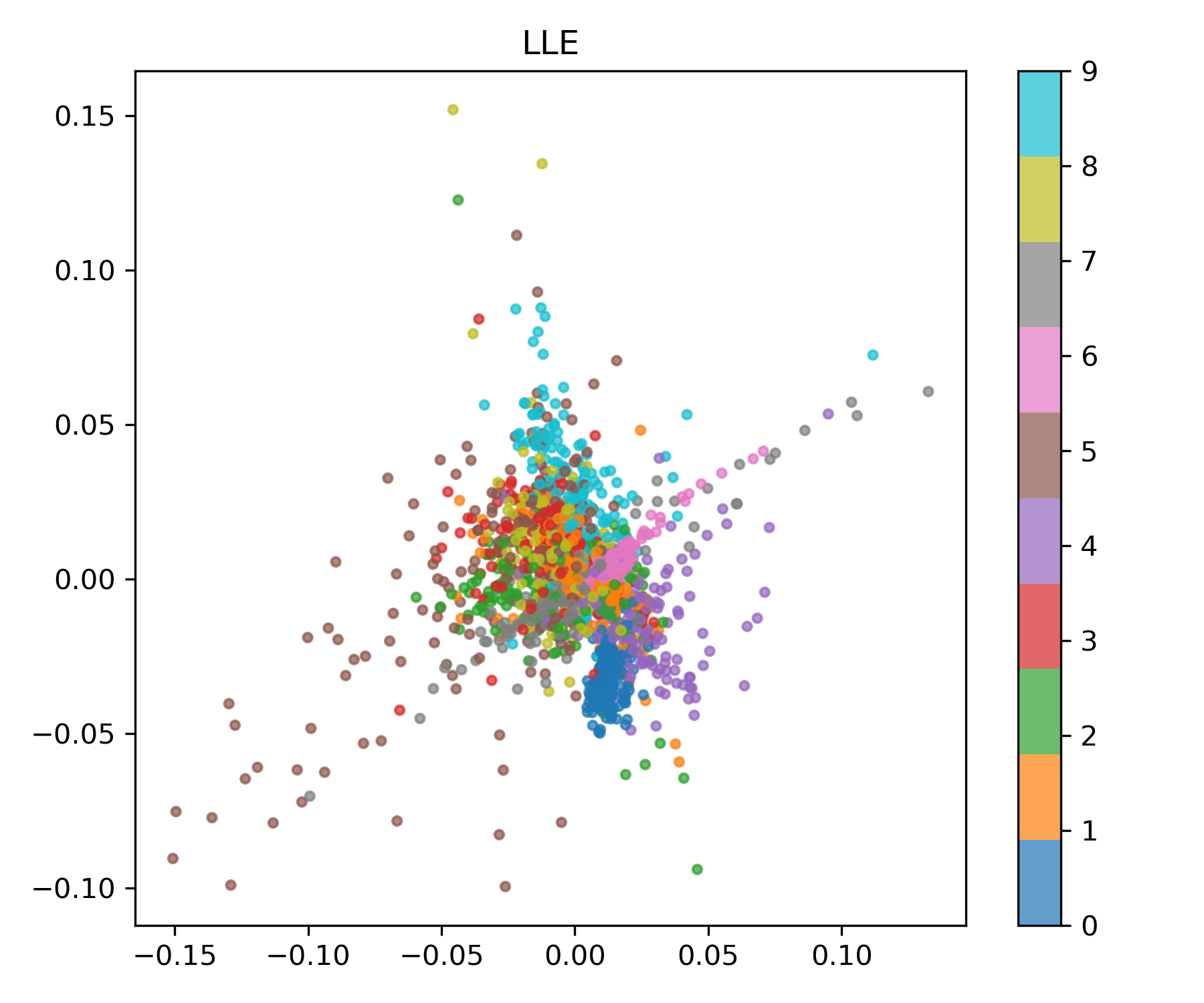
LLE (Locally Linear Embedding)

Kernel PCA는 전체적인 비선형 구조를 반영하지만, 국소적 구조(local structure) 를 보존하는 데는 한계가 있습니다.
LLE는 각 데이터가 이웃점의 선형 조합으로 표현된다는 가정하에 저차원 좌표를 찾습니다.

\[x_i \approx \sum_{j \in N(i)} w_{ij} x_j\]

lle = LocallyLinearEmbedding(n_neighbors=30, n_components=2, method="standard")
X_lle = lle.fit_transform(X)
plot_embedding(X_lle, y, "LLE", "lle.png")

Roweis & Saul, 2000

---

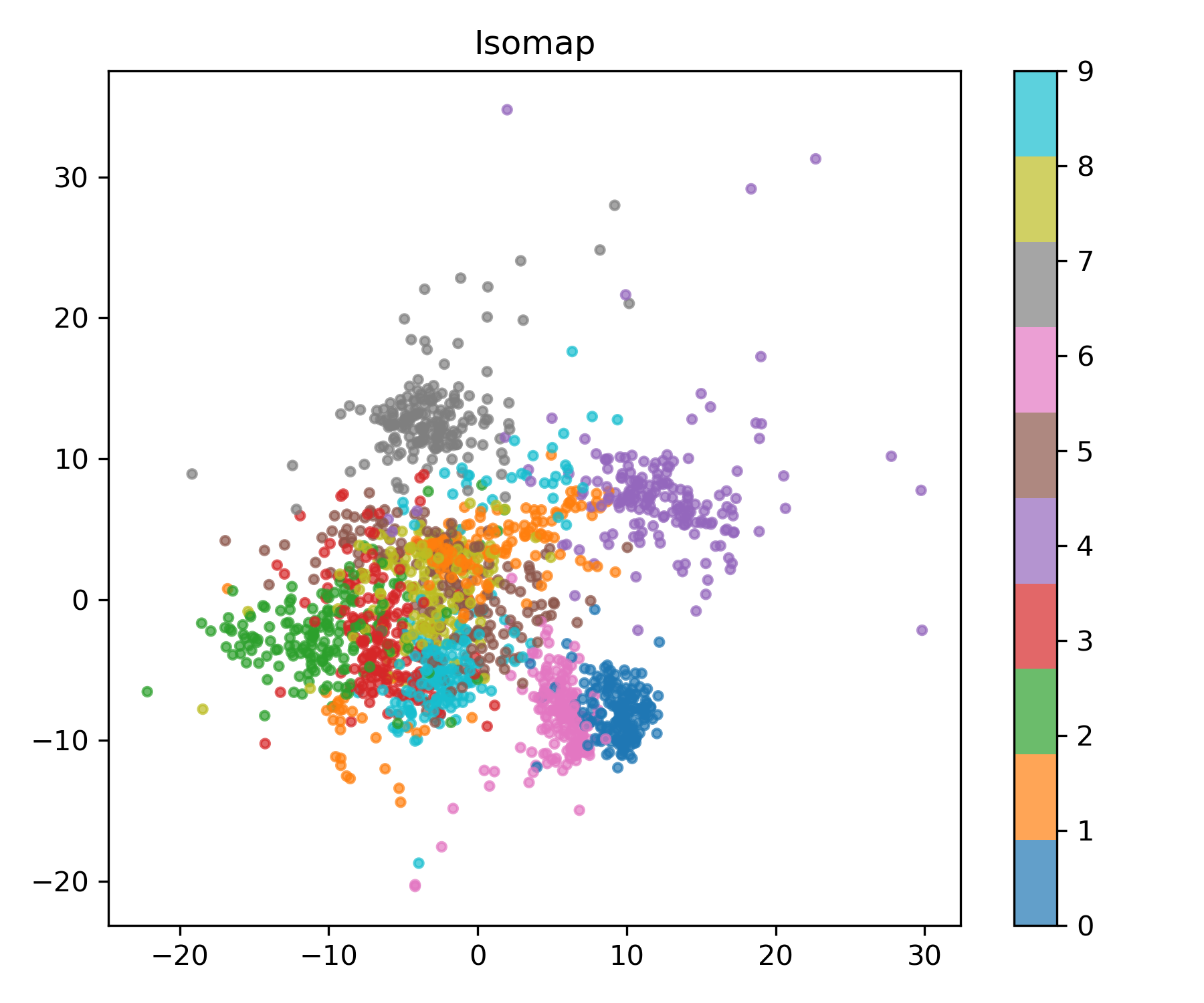
Isomap

LLE가 국소 구조를 강조한다면, Isomap은 전역적 곡면 구조를 학습합니다.
$k$-NN 그래프에서 지오데식 거리(매니폴드 위 최단 경로)를 계산하고, 이를 이용해 임베딩합니다.

isomap = Isomap(n_neighbors=30, n_components=2)
X_isomap = isomap.fit_transform(X)
plot_embedding(X_isomap, y, "Isomap", "isomap.png")

Tenenbaum et al., 2000

---

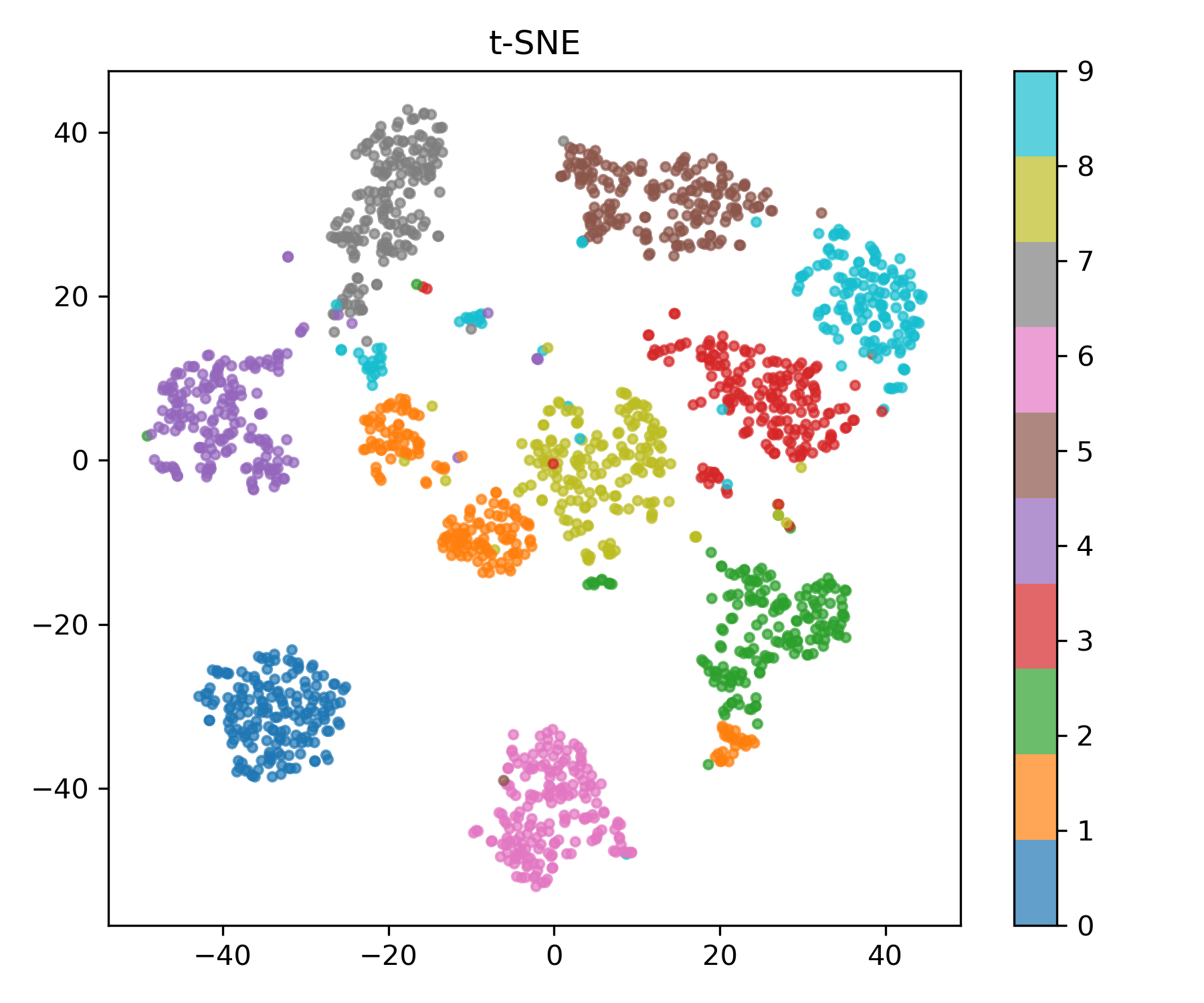
t-SNE (t-Distributed Stochastic Neighbor Embedding)

매니폴드 학습 계열은 구조를 잘 보존하지만, 시각화에 최적화된 기법은 아닙니다.
t-SNE는 고차원 이웃 확률분포 $P$와 저차원 확률분포 $Q$의 KL divergence를 최소화하여,
국소적 군집 구조를 시각화하는 데 탁월합니다.

tsne = TSNE(n_components=2, perplexity=30, random_state=42, init="pca", learning_rate="auto")
X_tsne = tsne.fit_transform(X)
plot_embedding(X_tsne, y, "t-SNE", "tsne.png")

van der Maaten & Hinton, 2008

---

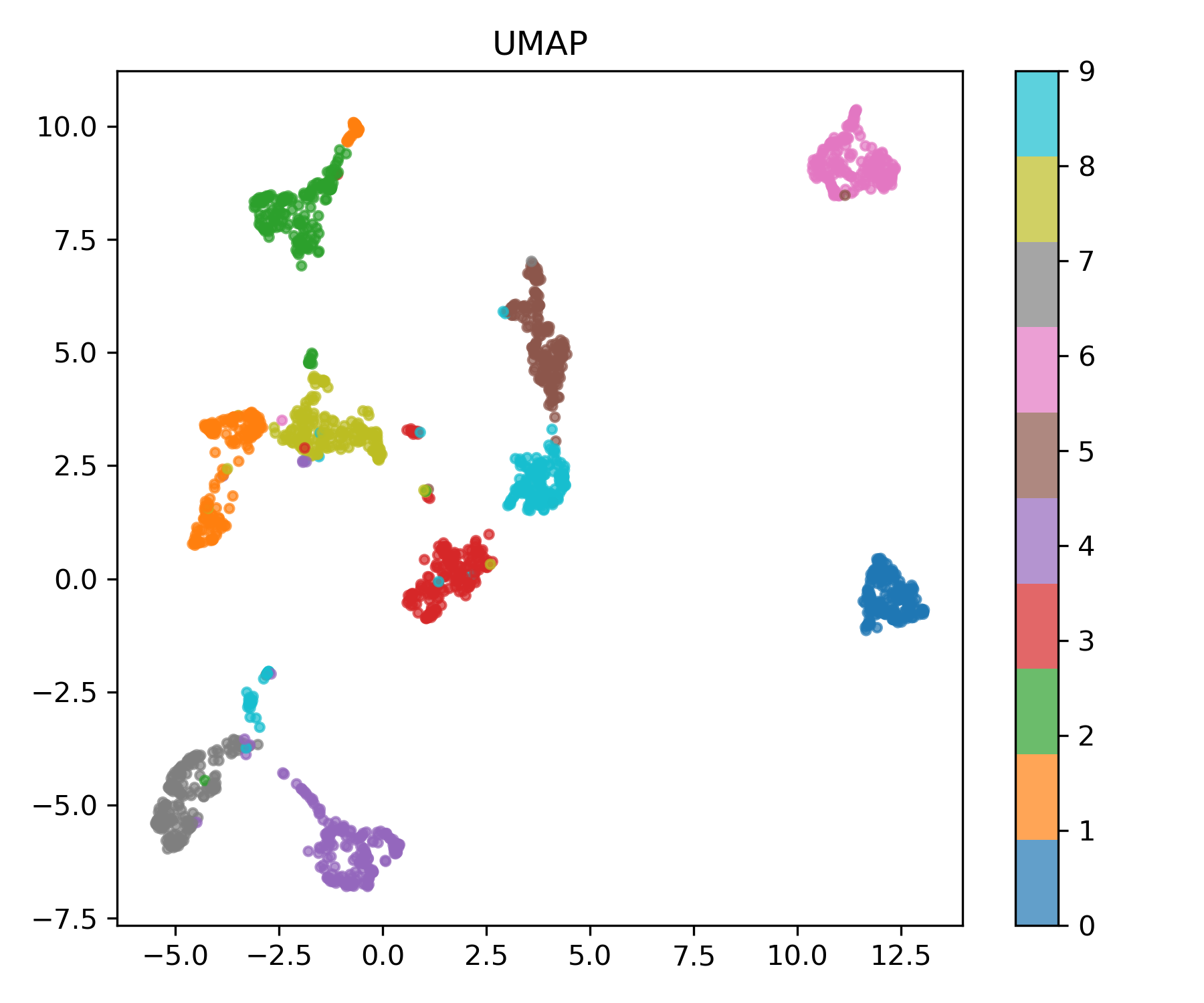
UMAP (Uniform Manifold Approximation and Projection)

마지막으로, t-SNE의 단점을 보완한 최신 기법 UMAP입니다.
t-SNE 대비 빠르고, 더 큰 데이터셋에도 적용 가능하며,
국소(local)와 전역(global) 구조를 균형 있게 보존합니다.

umap_model = umap.UMAP(n_components=2, random_state=42)
X_umap = umap_model.fit_transform(X)
plot_embedding(X_umap, y, "UMAP", "umap.png")

McInnes et al., 2018

---

Comparison Table

방법	선형성	확률적	불확실성 추론	비선형	지도학습	대표 응용
PCA	✅	❌	❌	❌	❌	데이터 압축, 시각화
PPCA	✅	✅	일부	❌	❌	Bayesian 해석
GPLVM	❌	✅	✅	✅	❌	고급 representation
LDA	✅	❌	❌	❌	✅	분류용 차원 축소
Kernel PCA	❌	❌	❌	✅	❌	비선형 구조
LLE	❌	❌	❌	✅	❌	국소 매니폴드 학습
Isomap	❌	❌	❌	✅	❌	곡면 구조 복원
t-SNE	❌	✅	❌	✅	❌	데이터 시각화
UMAP	❌	❌	❌	✅	❌	대규모 임베딩

---

Conclusion

차원 축소 기법은 단순한 시각화 도구를 넘어,
데이터의 본질적 구조를 파악하고 효율적인 학습을 가능케 하는 핵심 기법입니다.

• 선형 → 확률적/베이지안: PCA → PPCA → GPLVM
• 지도 차원 축소: LDA
• 비선형 확장: Kernel PCA → LLE → Isomap
• 최신 시각화: t-SNE, UMAP

데이터의 성격(선형/비선형, 지도/비지도, 소규모/대규모)에 따라
적절한 방법을 선택하는 것이 중요합니다.