Natural Gradient for Variational Inference

4 분 소요

이 포스팅은 Amari (1998)의 Natural Gradient 개념과
Variational Inference에서의 응용을 정리한 글입니다.

Introduction

일반적인 경사하강법(Gradient Descent)은 파라미터 공간을 유클리드 공간으로 간주합니다.
하지만 확률분포 최적화 문제에서는, 동일한 분포라도 파라미터화(parameterization) 방식에 따라 경사 방향이 달라지는 문제가 발생합니다.

이를 해결하기 위해 Amari (1998)는 자연 그래디언트(Natural Gradient) 를 제안했습니다.
이는 확률분포 공간의 정보 기하학적 구조(Fisher metric) 를 반영한, Parameterization에 불변한 최적화 방향입니다.

Ordinary Gradient vs. Natural Gradient

일반 Gradient 업데이트 $\theta \leftarrow \theta - \eta \nabla_\theta L(\theta)$
Natural Gradient 업데이트 $\theta \leftarrow \theta - \eta \, F(\theta)^{-1}\nabla_\theta L(\theta)$

여기서 $F(\theta)$는 Fisher Information Matrix입니다: $F(\theta) = \mathbb{E}\big[ \nabla_\theta \log p(y|\theta)\, \nabla_\theta \log p(y|\theta)^\top \big].$

Why Natural Gradient?

좌표 불변성: 파라미터화 방식이 달라져도 동일한 업데이트 방향
스케일 적응성: feature마다 다른 스케일을 자동으로 보정
빠른 수렴: Variational Bayes, 강화학습, Bayesian NN에서 안정적인 학습

Derivation via KL Constraint

자연 그래디언트는 “KL 반경을 일정하게 유지하면서 ELBO를 가장 빠르게 증가시키는 방향”으로 유도됩니다.
아래는 이를 한 줄 한 줄 증명한 과정입니다.

1. 국소 최적화 문제 설정

근사 분포 $q_\lambda(\theta)$가 있고,
최적화 목표는 $\mathcal L(\lambda)$ (예: ELBO).
변화량을 $\mathrm d\lambda$, 기울기를 $g := \nabla_\lambda \mathcal L(\lambda)$라 둡니다.

$\mathcal L$의 1차 테일러 근사: $\mathcal L(\lambda + \mathrm d\lambda) \;\approx\; \mathcal L(\lambda) + g^\top \mathrm d\lambda.$
KL 발산의 2차 근사: $\mathrm{KL}\!\big(q_\lambda \,\|\, q_{\lambda+\mathrm d\lambda}\big) \;\approx\; \tfrac12\, \mathrm d\lambda^\top F(\lambda)\, \mathrm d\lambda,$ 여기서 $F(\lambda) = \mathbb E_{q_\lambda}\!\big[\nabla_\lambda \log q_\lambda(\theta)\, \nabla_\lambda \log q_\lambda(\theta)^\top\big]$ 는 Fisher 정보 행렬입니다.
따라서 신뢰영역(trust region) 문제는: $\max_{\mathrm d\lambda}\; g^\top \mathrm d\lambda \quad \text{s.t.}\quad \tfrac12\,\mathrm d\lambda^\top F(\lambda)\,\mathrm d\lambda \le \varepsilon. \tag{*}$

2. 라그랑주 승수법 (KKT 조건)

라그랑지안 정의: $\mathcal J(\mathrm d\lambda,\alpha) = g^\top \mathrm d\lambda - \alpha\!\left(\tfrac12\,\mathrm d\lambda^\top F\,\mathrm d\lambda - \varepsilon\right), \quad \alpha \ge 0.$
정지조건(stationarity): $\nabla_{\mathrm d\lambda}\mathcal J = g - \alpha F \mathrm d\lambda = 0 \;\;\Longrightarrow\;\; F\,\mathrm d\lambda = \tfrac{1}{\alpha} g.$
따라서, $\mathrm d\lambda = \tfrac{1}{\alpha}\, F^{-1}\, g. \tag{A}$
제약 활성화(보완슬랙성): $\tfrac12\,\mathrm d\lambda^\top F\,\mathrm d\lambda = \varepsilon.$
(A)를 대입: $\tfrac12 \Big(\tfrac{1}{\alpha}F^{-1}g\Big)^\top F \Big(\tfrac{1}{\alpha}F^{-1}g\Big) = \varepsilon.$
정리하면: $\frac{1}{2\alpha^2}\, g^\top F^{-1} g = \varepsilon \quad\Longrightarrow\quad \alpha = \sqrt{\frac{g^\top F^{-1} g}{2\varepsilon}}.$

3. 최적 업데이트

따라서 최적 변화량은 $\mathrm d\lambda^\star = \kappa \, F^{-1} g,$ 여기서 $\kappa = 1/\alpha$는 학습률에 해당하는 상수입니다.

즉, 자연 그래디언트는 $\tilde{\nabla}_\lambda \mathcal L = F(\lambda)^{-1}\nabla_\lambda \mathcal L.$

4. 핵심 포인트

일반 gradient는 유클리드 공간에서의 “좌표 의존적” 기울기.
자연 gradient는 분포 공간의 KL 기하학(정보 기하학) 을 고려한 기울기.
따라서 파라미터화에 불변하며, 동시에 feature 스케일 차이도 자동으로 보정.

Visualization Examples

1. Quadratic Loss (Elliptical Gaussian NLL)

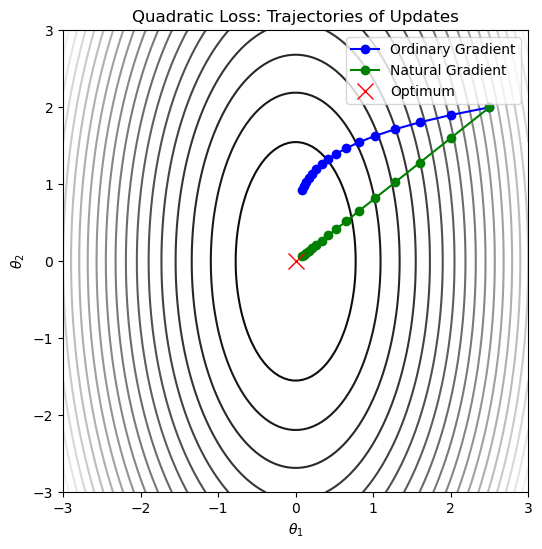
Quadratic Example

위 그림은 단순한 이차함수(quadratic) 에서 Ordinary Gradient(파란색)와 Natural Gradient(초록색)를 비교한 것입니다.

Ordinary Gradient는 좌표축 기준의 경사를 따라가기 때문에 곡선의 경로를 보입니다.
Natural Gradient는 Fisher metric을 반영하여 등고선을 따라 곧장 최적점으로 향하는 방향을 잡습니다.

2. Mixture of Gaussians Negative Log-Likelihood

Mixture of Gaussians Example

여기서는 두 개의 가우시안이 섞인 분포(Mixture of Gaussians) 의 음의 로그 가능도(NLL)를 최적화하는 상황입니다.

Ordinary Gradient는 곡선의 경로를 가지고 최적점을 향하는 모습을 보입니다.
Natural Gradient는 Fisher Information을 기반으로 분포의 지역적 곡률(local curvature) 을 반영하여, 더 안정적인 최적화 방향을 보여줍니다.

이 예시는 복잡한 확률분포에서도 Natural Gradient가 더 효율적임을 잘 보여줍니다.

Variational Inference와 Natural Gradient

Variational Inference(VI)는 복잡한 사후분포 $p(\theta|y)$를 tractable한 $q_\lambda(\theta)$로 근사하는 방법입니다.
최적화 목표는 ELBO (Evidence Lower Bound)입니다:

\[\mathcal{L}(\lambda) = \mathbb{E}_{q_\lambda}[\log p(y,\theta)] - \mathbb{E}_{q_\lambda}[\log q_\lambda(\theta)].\]

Ordinary Gradient의 한계

ELBO는 고차원 파라미터 공간에서 곡률이 심하게 다릅니다.
Ordinary Gradient는 parameterization과 스케일에 민감하여, 학습률 조정이 매우 까다롭습니다.
결과적으로 수렴 속도가 느리고 불안정합니다.

Natural Gradient의 역할

VI에서의 파라미터 $\lambda$는 분포 $q_\lambda$ 자체를 나타내므로,
자연스러운 거리 척도는 KL divergence입니다.
Natural Gradient는 이 KL geometry를 반영하여 불변성(invariance) 을 확보합니다.

즉, $\tilde{\nabla}_\lambda \mathcal L = F(\lambda)^{-1}\nabla_\lambda \mathcal L,$ 여기서 $F(\lambda)$는 $q_\lambda$의 Fisher 정보 행렬입니다.

Gaussian VI 예시

예를 들어, $q_\lambda(\theta) = \mathcal N(\mu, \Sigma), \quad \lambda = (\mu, \Sigma).$

Ordinary Gradient로는 $\Sigma$ 업데이트가 수치적으로 불안정해질 수 있습니다.
Natural Gradient는 KL geometry를 따라 업데이트하므로,
$\mu$와 $\Sigma$ 모두 안정적이고 효율적으로 최적화됩니다.

파이썬 코드

import numpy as np
import matplotlib.pyplot as plt

# 타겟분포 p(theta) = N(3, 1)
mu_p, sigma_p = 3.0, 1.0

# 파라미터 초기화
mu, log_sigma = -2.0, 1.0
lr = 0.1
steps = 100

traj_grad, traj_natgrad = [], []

def kl_divergence(mu, sigma2):
    return 0.5 * ((mu - mu_p)**2 / sigma_p**2 + sigma2/sigma_p**2 - 1 + np.log(sigma_p**2/sigma2))

for method in ["grad", "natgrad"]:
    mu, sigma2 = -2.0, np.exp(1.0)

    traj = []
    for t in range(steps):
        traj.append((mu, np.sqrt(sigma2)))

        grad_mu = (mu - mu_p) / sigma_p**2
        grad_sigma2 = 0.5 * (1/sigma_p**2 - 1/sigma2)

        if method == "grad":
            mu -= lr * grad_mu
            sigma2 -= lr * grad_sigma2
        else:
            nat_grad_mu = sigma2 * grad_mu
            nat_grad_sigma2 = 2 * sigma2**2 * grad_sigma2
            mu -= lr * nat_grad_mu
            sigma2 -= lr * nat_grad_sigma2

        sigma2 = max(sigma2, 1e-6)

    if method == "grad":
        traj_grad = traj
    else:
        traj_natgrad = traj

mus = np.linspace(-2, 5, 100)
sigs = np.linspace(0.2, 2.5, 100)
M, S = np.meshgrid(mus, sigs)
KL = np.array([[kl_divergence(m, s**2) for m in mus] for s in sigs])

plt.figure(figsize=(8,6))
cs = plt.contour(M, S, KL, levels=20, cmap="gray")
plt.clabel(cs, inline=True, fontsize=8)

plt.plot([m for m,s in traj_grad], [s for m,s in traj_grad], 'o-', label="Ordinary Gradient")
plt.plot([m for m,s in traj_natgrad], [s for m,s in traj_natgrad], 'o-', label="Natural Gradient")
plt.scatter([mu_p], [sigma_p], c="red", s=120, marker="*", label="True Posterior")

plt.xlabel("Mean (mu)")
plt.ylabel("Std (sigma)")
plt.title("Gaussian VI: Gradient vs Natural Gradient")
plt.legend()
plt.grid()
plt.show()

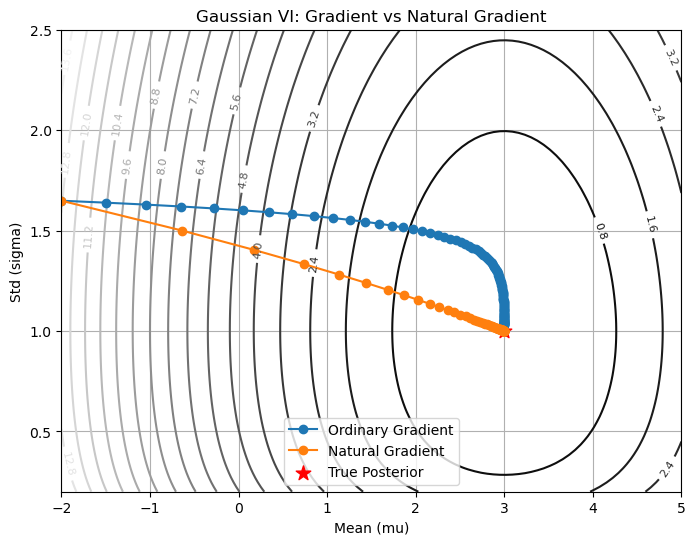
Gaussian Variational Inference

위 그림은 Gaussian Variational Inference를 Ordinary Gradient와 Natural Gradient 각각을 파이썬으로 구현하여 시각화한 예시입니다.

배경 등고선 (검은 곡선) KL divergence $\mathrm{KL}(q||p)$ 값의 등고선입니다. 안쪽으로 갈수록 값이 작아지며, 실제 posterior $\mathcal N(3,1)$에서 최소가 됩니다.
파란 경로 (Ordinary Gradient)
- 초기값에서 출발해 지그재그로 이동합니다.
- 이유: Ordinary Gradient는 단순히 좌표축 기준으로 업데이트하기 때문에, 평균 $\mu$와 분산 $\sigma^2$의 스케일 차이를 보정하지 못합니다.
- 결과적으로 불필요하게 돌아가는 경로를 탑니다.
주황 경로 (Natural Gradient)
- Fisher Information metric을 이용해 스케일 차이를 자동으로 보정합니다.
- $\sigma$ 방향으로는 보폭을 줄이고, $\mu$ 방향으로는 보폭을 키워 효율적으로 이동합니다.
- 그 결과, 곧장 빨간 별 로 안정적이고 빠르게 수렴합니다.

Intuition

일반 gradient: 단순히 좌표축 기준의 기울기
자연 gradient: 분포 공간에서의 진짜 경사 방향
Fisher Information: “민감한 방향은 줄이고, 둔감한 방향은 키워주는 스케일링 역할”

Conclusion

Natural Gradient는 Variational Inference, 강화학습, Bayesian Deep Learning 등에서 필수적인 도구
분포의 기하학적 구조를 반영해 더 효율적이고 안정적인 최적화를 제공

Reference

X Facebook LinkedIn Bluesky

Junhee Kim

추천 포스트